
分析 将y=x-4和y=$\frac{2}{x}$联立方程组,求得方程组的解,根据直线y=x-4和双曲线y=$\frac{2}{x}$的一个交点为(a,b),然后分类讨论,即可求得$\frac{1}{b}-\frac{1}{a}$的值.
解答 解:$\left\{\begin{array}{l}{y=x-4}\\{y=\frac{2}{x}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=2+\sqrt{6}}\\{y=\sqrt{6}-2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2-\sqrt{6}}\\{y=-2-\sqrt{6}}\end{array}\right.$,
∵直线y=x-4和双曲线y=$\frac{2}{x}$的一个交点为(a,b),
∴当a=$2+\sqrt{6}$,b=$\sqrt{6}$-2时,$\frac{1}{b}-\frac{1}{a}=\frac{1}{\sqrt{6}-2}-\frac{1}{2+\sqrt{6}}$=$\frac{\sqrt{6}+2}{2}-\frac{\sqrt{6}-2}{2}=2$,
当a=2-$\sqrt{6}$,b=-2-$\sqrt{6}$时,$\frac{1}{b}-\frac{1}{a}$=$\frac{1}{-2-\sqrt{6}}-\frac{1}{2-\sqrt{6}}$=$\frac{-(\sqrt{6}-2)}{2}+\frac{\sqrt{6}+2}{2}$=2,
由上可得,$\frac{1}{b}-\frac{1}{a}$=2,
故答案为:2.
点评 本题考查反比例函数与一次函数的交点问题,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用分类讨论的数学思想解答.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
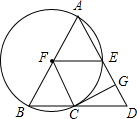 如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
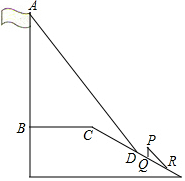 某中学广场上的旗杆AB,在某一时刻它的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为3米,落在斜坡上的影长CD为2米,AB⊥BC,同一时刻,光线与水平面的夹角为60°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(若结果中有根号,请保留根号)
某中学广场上的旗杆AB,在某一时刻它的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为3米,落在斜坡上的影长CD为2米,AB⊥BC,同一时刻,光线与水平面的夹角为60°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(若结果中有根号,请保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com