
分析 (1)将已知条件代入代数式求值即可;
(2)将$A=\frac{p+q}{2}$,$G=\sqrt{pq}$,$\frac{1}{p}-\frac{1}{H}=\frac{1}{H}-\frac{1}{q}$变形后即可确定三者之间的关系;
(3)列树状图将所有等可能的结果列举出来,利用概率公式求解即可.
解答 解:(1)∵p=2,q=6,
∴$A=\frac{p+q}{2}$=$\frac{2+6}{2}$=4,$G=\sqrt{pq}$=$\sqrt{12}$=2$\sqrt{3}$,H=3,
故答案为:4,2$\sqrt{3}$,3;
(2)∵$A=\frac{p+q}{2}$,$G=\sqrt{pq}$,$\frac{1}{p}-\frac{1}{H}=\frac{1}{H}-\frac{1}{q}$,
∴$\frac{2}{H}$=$\frac{p+q}{pq}$,
∴H=$\frac{2pq}{p+q}$=$\frac{{G}^{2}}{A}$,
∴G2=AH;
(3)列树状图如下: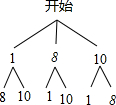
∵一共有6种情况,其中10,8,$\frac{32}{5}$是平均数组,共2种满足条件,
∴P(构成平均数组)=$\frac{2}{6}$=$\frac{1}{3}$.
点评 考查了列表及树状图的方法,解题的关键是根据题意将所有等可能的结果列举出来,难度不大.


科目:初中数学 来源: 题型:填空题
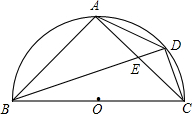 如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.
如图,BC为半圆的直径,O为圆心,D是弧AC的中点,四边形ABCD的对角线AC,BD交于点E,BC=$\frac{5}{2}$,CD=$\frac{{\sqrt{5}}}{2}$,则sin∠AEB的值为$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
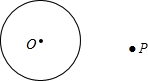 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
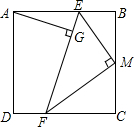 已知,在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,交射线CD于点F,AB=4,当DF=1时,求点A到直线EF的距离.
已知,在正方形ABCD中,M是边BC中点,E是边AB上的一个动点,MF⊥ME,交射线CD于点F,AB=4,当DF=1时,求点A到直线EF的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com