
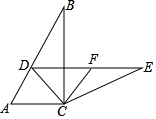
 如图,在Rt△ABC 中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,得到△DEC,若点D刚好落在AB边上,取DE边的中点F,连接FC,判断四边形ACFD的形状,并说明理由.
如图,在Rt△ABC 中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转,得到△DEC,若点D刚好落在AB边上,取DE边的中点F,连接FC,判断四边形ACFD的形状,并说明理由. 分析 由在Rt△ABC 中,∠ACB=90°,∠B=30°,易得△ACD是等边三角形,则可得AC=AD=$\frac{1}{2}$AB,又由旋转的性质与直角三角形斜边的中线的性质,证得DF=CF=$\frac{1}{2}$DE,则可得AC=CF=DF=AD,继而证得四边形ACFD是菱形.
解答 解:四边形ACFD是菱形.
理由:∵在Rt△ABC 中,∠ACB=90°,∠B=30°,
∴∠A=90°-∠B=60°,AC=$\frac{1}{2}$AB,
∵将△ABC绕点C按顺时针方向旋转,得到△DEC,
∴CA=CD,AB=DE,∠ACB=∠DCE=90°,
∴△ACD是等边三角形,
∴AC=AD,
∵F是DE的中点,
∴DF=CF=$\frac{1}{2}$DE,
∴AC=CF=DF=AD,
∴四边形ACFD是菱形.
点评 此题考查了旋转的性质、菱形的判定、含30°直角三角形的性质以及直角三角形斜边上的中线的性质.注意证得AC=CF=DF=AD是关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
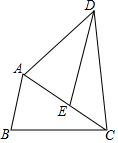 如图,在△ABC中,点E是AC上一点,AE=AB,过点E作DE∥AB,且DE=AC.
如图,在△ABC中,点E是AC上一点,AE=AB,过点E作DE∥AB,且DE=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
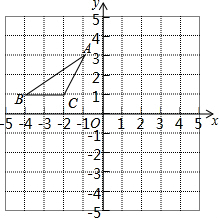 在平面直角坐标系中,△ABC的位置如图所示,A、B、C三点的坐标分别为A(-1,3)、B(-4,1)、C(-2,1),把△ABC向右平移4个单位长度后得到对应的△A1B1C1,再将△A1B1C1向下平移5个单位长度后得到对应的△A2B2C2.
在平面直角坐标系中,△ABC的位置如图所示,A、B、C三点的坐标分别为A(-1,3)、B(-4,1)、C(-2,1),把△ABC向右平移4个单位长度后得到对应的△A1B1C1,再将△A1B1C1向下平移5个单位长度后得到对应的△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com