
【题目】如图,正方形ABCD中,点E为AB上一动点(不与A、B重合).将△EBC沿CE翻折至△EFC,延长EF交边AD于点G.
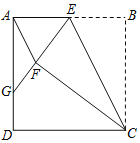
(1)连结AF,若AF∥CE.证明:点E为AB的中点;
(2)证明:GF=GD;
(3)若AD=5,设EB=x,GD=y,求y与x的函数关系式.
【答案】(1)见解析;(2)见解析;(3)y=![]()
【解析】
(1)由翻折的性质可知,∠BEC=∠FEC,EB=EF,根据平行线的性质和等量代换可证得∠EAF=∠EFA,从而可得EA=EF,进而可得结论;
(2)如图所示,连接CG,由正方形的性质和折叠的性质可得DC=FC,∠GFC=∠D=90°,从而可利用HL证明Rt△GFC≌Rt△GDC,进而可得结论;
(3)根据题意可用含x、y的代数式表示出AG,AE,GE,然后在Rt△AEG中由勾股定理即可得出结果.
解:(1)证明:由翻折的性质可知,∠BEC=∠FEC,EB=EF,
∵AF∥CE,
∴∠BEC=∠EAF,∠FEC=∠EFA,
∴∠EAF=∠EFA,
∴EA=EF.
∴EA=EB,即点E为AB的中点;
(2)证明:如图所示,连接CG.
∵四边形ABCD是正方形,
∴∠D=∠B=90°,DC=BC,
由翻折的性质可知:∠EFC=∠B=90°,BC=FC,
∴∠GFC=∠D=90°,FC=DC,
又∵CG=CG,
∴Rt△GFC≌Rt△GDC(HL),
∴GF=GD;
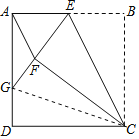
(3)∵AD=5,EB=x,GD=y,
∴AG=5﹣y,AE=5﹣x,GE=x+y,
则在Rt△AEG中,∵AG2+AE2=GE2,
∴(5﹣y)2+(5﹣x)2=(x+y)2,
整理,得:y=![]() ,
,
即y与x的函数关系式是y=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )

A. DE=EB B. ![]() DE=EB C.
DE=EB C. ![]() DE=DO D. DE=OB
DE=DO D. DE=OB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;
(4)身高在![]() 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x1、x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:![]() ,
,![]() .我们把它们称为根与系数关系定理.
.我们把它们称为根与系数关系定理.
如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:AB=![]() =
=![]() =
=![]() =
=![]() =
=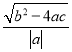
请你参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时,直接写出b2-4ac的值;
(2)当△ABC为等腰三角形,且∠ACB=120°时,直接写出b2-4ac的值;
(3)设抛物线y=x2+mx+5与x轴的两个交点为A、B,顶点为C,且∠ACB=90°,试问如何平移此抛物线,才能使∠ACB=120°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边AD上的一点,将△DEC沿CE折叠至△D′EC处,若∠B=48°,∠ECD=25°,则∠D′EA的度数为( )

A.33°B.34°C.35°D.36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图像相交于点
的图像相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求![]() 的值和
的值和![]() 的值以及点
的值以及点![]() 的坐标;
的坐标;
(2)观察反比例函数![]() 的图像,当
的图像,当![]() 时,请直接写出自变量
时,请直接写出自变量![]() 的取值范围;
的取值范围;
(3)以![]() 为边作菱形
为边作菱形![]() ,使点
,使点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在第一象限,求点
在第一象限,求点![]() 的坐标;
的坐标;
(4)在y轴上是否存在点![]() ,使
,使![]() 的值最小?若存在,请求出点
的值最小?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个一次函数的图象与x轴交于同一点,则称这两个函数为一对“x牵手函数”,这个交点为“x牵手点”.
(1)一次函数y=x﹣1与x轴的交点坐标为 ;一次函数y=ax+2与一次函数y=x﹣1为一对“x牵手函数”,则a= ;
(2)已知一对“x牵手函数”:y=ax+1与y=bx﹣1,其中a,b为一元二次方程x2﹣kx+k﹣4=0的两根,求它们的“x牵手点”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,等边△AEF的顶点E、F分别在BC和CD上.
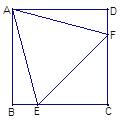
(1)、求证:△ABE≌△ADF;
(2)、若等边△AEF的周长为6,求正方形ABCD的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com