
【题目】快车与慢车分別从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留 1h,然后按原路原速返回, 快车比慢车晚 1h 到达甲地,快慢两车距各自出发地的路程 y(km)与所用的时间 x(h)的关系如图所示.
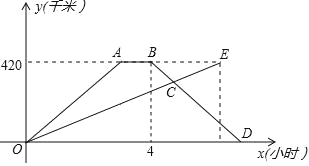
(1)甲乙两地之间的路程为 km;快车的速度为 km/h;慢车的速度为 km/h ;
(2)出发 h,快慢两车距各自出发地的路程相等;(写出解答过程快慢两车出发 h 相距 150km.(写出解答过程)
【答案】(1)420;140;70(2)![]() ;
;![]() 或
或![]() 或
或![]()
【解析】
(1)先得两地的距离,根据速度=路程÷时间列式计算即可求出快车和慢车的速度;
(2)由图可知:快车返程时,两车距各自出发地的路程相等,根据慢车的路程=2个总路程快车的路程,列方程即可得出答案;分别根据两车相遇以及两车相遇后两车距离为150km时,列方程可解答.
(1)由图可知:甲乙两地之间的路程为420km;
快车的速度为:![]() =140km/h;
=140km/h;
由题意得:快车7小时到达甲地,则慢车6小时到达甲地,
则慢车的速度为:![]() =70km/h;
=70km/h;
故答案为:420,140,70;
(2)∵快车速度为:140km/h,
∴A点坐标为;(3,420),
∴B点坐标为(4,420),
由图可知:快车返程时,两车距各自出发地的路程相等,
设出发x小时,两车距各自出发地的路程相等,
70x=2×420140(x1),
70x=98014x,
解得:x=![]() ,
,
答:出发![]() 小时,快、慢两车距各自出发地的路程相等;
小时,快、慢两车距各自出发地的路程相等;
故答案为:![]() ;
;
第一种情形第一次没有相遇前,相距150km,
则140x+70x+150=420,
解得:x=![]() ,
,
第二种情形应是相遇后而快车没到乙地前140x+70x420=150,
解得:x=![]() ,
,
第三种情形是快车从乙往甲返回:70x140(x4)=150,
解得:x=![]() ,
,
综上所述:快慢两车出发![]() h或
h或![]() h或
h或![]() h相距150km.
h相距150km.
故答案为:![]() 或
或![]() 或
或![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
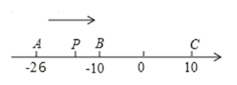
【题目】已知数轴上有 A、B、C 三点,分别表示有理数-26,-10,10,动点 P 从 A 出发,以每秒 1 个 单位的速度向终点 C 移动,设点 P 移动时间为 t 秒.
(1)用含 t 的代数式表示 P 到点 A 和点C 的距离:PA= ,PC=
(2)当点 P 运动到 B 点时,点 Q 从 A 点出发,以每秒 3 个单位的速 度向 C 点运动,Q 点到达 C 点后,再立即以同样的速度返回,当点 P 运动到点 C 时,P、Q 两点运动停止,
①当 P、Q 两点运动停止时,求点 P 和点 Q 的距离;
②求当 t 为何值时 P、Q 两点恰好在途中相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AE⊥BC于E,AF⊥CD于F.
(1)点A到直线BC的距离是线段_______的长;
(2)点D到直线AF的距离是线段_______的长;
(3)线段AF的长表示点A到直线_______距离;
(4)线段CE的长表示点C到直线_______距离;
(5)线段BE的长表示点_______到直线______距离;
(6)线段CF的长表示点_______到直线______距离;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() (a 0,且 a1,m、n 是整数),则 m n.你能利用上面的结论解决下面的问题吗?
(a 0,且 a1,m、n 是整数),则 m n.你能利用上面的结论解决下面的问题吗?
(1)如果 2 8![]() 16
16![]() 2
2![]() ,求 x 的值;
,求 x 的值;
(2)如果![]() ,求 x 的值.
,求 x 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了把赣州建成文明城市,市政府在每个红绿灯处设置了志愿者文明监督岗,志愿者老刘某天在市内的一个十字路口,对行人及骑自行车和电动车闯红灯的人数进行了统计.统计方法如下:
①时间:上午7:00~12:00,分5个时间段,每个时间段时长为1小时;
②在每个时间段里,随机选择一个红绿灯周期,每个红绿灯周期是90秒;
③对闯红灯和未闯红灯的人数进行统计.
下图是志愿者老刘对各时间段的一个红绿灯周期内闯红灯的人数制作的条形统计图和扇形统计图,但均不完整.请你根据统计图解答下列问题.
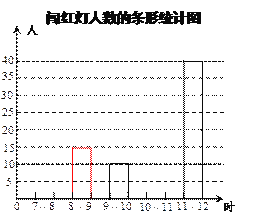

(1)估计这一天上午7:00~12:00在这个十字路口共有多少人闯红灯;
(2)请你把条形统计图补充完整;
(3)志愿者老刘统计,各时间段的一个红绿灯周期内闯红灯的人数占通过该十字路口人数的百分比依次是:15%,20%,12%,15%,25%.这一天上午7:00~12:00这一时间段中,该十字路口平均每小时大约有多少人通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 与
与![]() 成正比例,且
成正比例,且![]() 时,
时,![]() .
.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)将所得函数图象平移,使它过点(2, -1).求平移后直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )

A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形A`B`C`是由三角形ABC经过某种平移得到的,点A与点A`,点B与点B`,点C与点C`分别对应,观察点与点坐标之间的关系,解答下列问题:

![]() 分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
![]() 若点
若点![]() 是点
是点![]() 通过
通过![]() 中的平移变换得到的,求
中的平移变换得到的,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com