【题目】如图，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案．已知大正方形面积为49，小正方形面积为4，若用
，
表示直角三角形的两直角边
，下列四个说法：①
；②
；③
；④
；其中说法正确的是
A. ①②B. ①②③C. ①②④D. ①②③④
【答案】D
【解析】
大正方形的面积是49，则其边长是7，显然，利用勾股定理可得①x2+y2=49；小正方形的面积是4，则其边长是2，根据图可发现y+2=x，即②x-y=2；其中④由2xy+4=49可得2xy=45①，又由x2+y2=49②，可得
；还可以得出四个三角形的面积+小正方形的面积=大正方形的面积，即
，化简得④2xy+4=49；从而求解．
解：如图
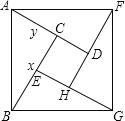
①
为直角三角形，
根据勾股定理：
，
故本选项正确；
②由图可知，
，
故本选项正确；
③由
可得
①，
又
②，
①
②得，
，
整理得，
，
，
故本选项正确．
④由图可知，四个直角三角形的面积与小正方形的面积之和为大正方形的面积，列出等式为，
即；
故本选项正确；
正确结论有①②③④．
故选：
．
名校课堂系列答案科目：初中数学 来源： 题型：
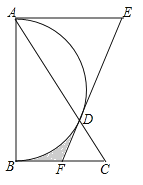
【题目】（2017湖北省恩施州）如图，在Rt△ABC中，∠BAC=30°，以直角边AB为直径作半圆交AC于点D，以AD为边作等边△ADE，延长ED交BC于点F，BC=
，则图中阴影部分的面积为______．（结果不取近似值）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】设a，b，c是△ABC的三条边，关于x的方程
x2+
x+c-a=0有两个相等的实数根，方程3cx+2b=2a的根为x=0.
（1）试判断△ABC的形状；
（2）若a，b为方程x2+mx-3m=0的两个根，求m的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中，x与y的部分对应值如下表：
x | ﹣3 | ﹣2 | ﹣1 | 0 |
y | 0 | ﹣3 | ﹣4 | ﹣3 |
下列结论：
①ac＜0；
②当x＞1时，y随x的增大而增大；
③﹣4是方程ax2+（b﹣4）x+c=0的一个根；
④当﹣1＜x＜0时，ax2+（b﹣1）x+c+3＞0．其中正确结论的个数为（ ）
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于整式
（其中m是大于
的整数）.
（1）若
，且该整式是关于x的三次三项式，求m的值；
（2）若该整式是关于x的二次单项式，求m，n的值；
（3）若该整式是关于x的二次二项式，则m，n要满足什么条件？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走60 m到达点C，测得点B在点C的北偏东60°方向，如图②.
(1)求∠CBA的度数；
(2)求出这段河的宽(结果精确到1 m，参考数据：
≈1.41，
≈1.73)．
① ②
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线a∥b，依次有3个三角形放置在上面，它们分别是等边三角形、等腰直角三角形、含30°角的直角三角形，直接填写出∠1、∠2、∠3 的度数.
∠1= °;∠2= °;∠3= °.
查看答案和解析>>
科目：初中数学 来源： 题型：
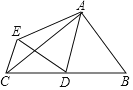
【题目】如图，△ABC中，∠BAC=90°，AB=3，AC=4，点D是BC的中点，将△ABD沿AD翻折得到△AED，连CE，则线段CE的长等于（ ）
A.2B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠xOy=90°，线段AB=10，若点A在Oy上滑动，点B随着线段AB在射线Ox上滑动(A，B与O不重合)，Rt△AOB的内切圆☉K分别与OA，OB，AB切于点E，F，P.
(1)在上述变化过程中，Rt△AOB的周长，☉K的半径，△AOB外接圆半径，这几个量中不会发生变化的是什么?并简要说明理由.
(2)当AE=4时，求☉K的半径r.
(3)当Rt△AOB的面积为S，AE为x，试求S与x之间的函数关系，并求出S最大时直角边OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com