
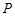 的横坐标,将它所对的面的数字作为点
的横坐标,将它所对的面的数字作为点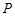 的纵坐标,则点
的纵坐标,则点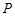 落在抛物线
落在抛物线 与
与 轴所围成的区域内(不含边界)的概率是 .
轴所围成的区域内(不含边界)的概率是 .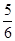 .
.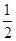 x2+6与x轴所围成的区域内(不含边界)的是有可能情况,即可得到P落在抛物线内的概率.
x2+6与x轴所围成的区域内(不含边界)的是有可能情况,即可得到P落在抛物线内的概率.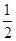 x2+6,
x2+6, 或2
或2 ,
, <x<2
<x<2 ,
,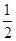 x2+6与x轴所围成的区域内(不含边界)有(-1,2)、(-2,0)、(0,1)、(2,-1)、(0,1),
x2+6与x轴所围成的区域内(不含边界)有(-1,2)、(-2,0)、(0,1)、(2,-1)、(0,1),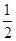 x2+6与x轴所围成的区域内(不含边界)的概率=
x2+6与x轴所围成的区域内(不含边界)的概率=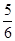 .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源:不详 题型:解答题
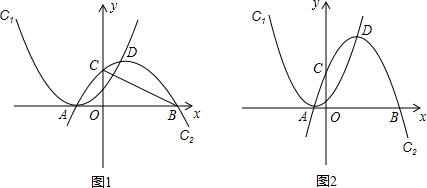
 .
. ﹣m(0<m<
﹣m(0<m< )时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
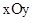 中,二次函数
中,二次函数 (
( )的图象与
)的图象与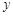 轴正半轴交于A点.
轴正半轴交于A点.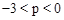 时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
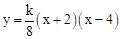 (
(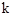 为常数,且
为常数,且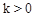 )与
)与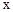 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与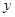 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线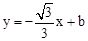 与抛物线的另一交点为D.
与抛物线的另一交点为D.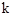 的值;
的值;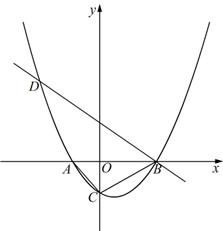
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象与x轴有两个公共点,那么一元二次方程
的图象与x轴有两个公共点,那么一元二次方程 有两个不相等的实数根.”据此判断方程x2-2x=
有两个不相等的实数根.”据此判断方程x2-2x= -2实数根的情况是 ( )
-2实数根的情况是 ( )| A.有三个实数根 | B.有两个实数根 | C.有一个实数根 | D.无实数根 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com