
����Ŀ����������ABCD�ı�AB����ȡһ��E����EF��AB��BD�ڵ�F��ȡFD���е�G������EG��CG����ͼ��1������֤ EG=CG��EG��CG��
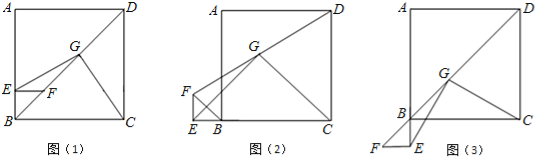
��1������BEF�Ƶ�B��ʱ����ת90������ͼ��2�������߶�EG��CG��������������ϵ��λ�ù�ϵ����ֱ��д����IJ��룮
��2������BEF�Ƶ�B��ʱ����ת180������ͼ��3�������߶�EG��CG����������������ϵ��λ�ù�ϵ����д����IJ��룬������֤����
���𰸡�
�⣨1��EG="CG " EG��CG------------------------------------------------------------(2��)
��2��EG="CG " EG��CG------------------------------------------------------------(2��)
֤�����ӳ�FE��DC�ӳ�����M����MG
�ߡ�AEM=90������EBC=90������BCM=90��
���ı���BEMC�Ǿ���.
��BE=CM����EMC=90��
����BE=EF
��EF=CM
�ߡ�EMC=90����FG=DG
��MG=![]() FD=FG
FD=FG
��BC="EM" ��BC=CD
��EM=CD
��EF=CM
��FM=DM
���F=45��
��FG=DG
�ߡ�CMG=![]() ��EMC=45��
��EMC=45��
���F=��GMC
���GFE�ա�GMC
��EG="CG" ����FGE=��MGC------------------------------------------------------------------------(2��)
�ߡ�FMC=90����MF=MD�� FG="DG"
��MG��FD
���FGE+��EGM=90��
���MGC+��EGM=90��
����EGC=90��
��EG��CG------------------------------------------------------------------------------------------- (2��)
��������
�����ͼ��1����Ѱ��֤�����۵�˼·���ӳ�FE��DC����M����MG���������GFE�ա�GMC���ý��ۣ���ͼ��2������3���н���˽֤ⷨ����
�⣺��1��EG=CG��EG��CG��
��2��EG=CG��EG��CG��
֤�����ӳ�FE��DC�ӳ�����M����MG��
�ߡ�AEM=90������EBC=90������BCM=90����
���ı���BEMC�Ǿ��Σ�
��BE=CM����EMC=90����
��ͼ��3����֪��
��BDƽ����ABC����ABC=90����
���EBF=45����
����EF��AB��
���BEFΪ����ֱ��������
��BE=EF����F=45����
��EF=CM��
�ߡ�EMC=90����FG=DG��
��MG=![]() FD=FG��
FD=FG��
��BC=EM��BC=CD��
��EM=CD��
��EF=CM��
��FM=DM��
����FG=DG��
��CMG=![]() ��EMC=45����
��EMC=45����
���F=��GMC��
������GFE����GMC�� ��
��
���GFE�ա�GMC��SAS����
��EG=CG����FGE=��MGC.
�ߡ�FMC=90����MF=MD��FG=DG��
��MG��FD��
���FGE+��EGM=90����
���MGC+��EGM=90����
����EGC=90����
��EG��CG��



 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����̨��ѩ�Ƕ������˻������Ŀ֮һ���˶�Ա������ķ���·�߿��Կ����������ߵ�һ���֣��˶�Ա���������ֱ�߶�y����λ��m����ˮƽ����x����λ��m���������㺯����ϵy��ax2+bx+c��a��0������ͼ��¼��ij�˶�Ա�������x��y���������ݣ�������������ģ�ͺ����ݣ����ƶϳ����˶�Ա��������е���ߵ�ʱ��ˮƽ����Ϊ�� ��
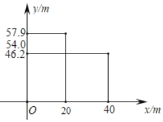
A. 10mB. 20mC. 15mD. 22.5m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�![]() ��
��![]() ���Խ���AC��BD���ڵ�
���Խ���AC��BD���ڵ�![]() ��P�ӵ�A��������AD���������˶����ٶ�Ϊ
��P�ӵ�A��������AD���������˶����ٶ�Ϊ![]() ��ͬʱ����Q�ӵ�D��������DC���������˶����ٶ�Ϊ
��ͬʱ����Q�ӵ�D��������DC���������˶����ٶ�Ϊ![]() ����һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶�
����һ����ֹͣ�˶�ʱ����һ����Ҳֹͣ�˶�![]() ����PO���ӳ�����BC�ڵ�E������Q��
����PO���ӳ�����BC�ڵ�E������Q��![]() ����BD�ڵ�
����BD�ڵ�![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ������������⣺
������������⣺
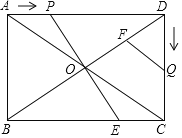
��1����tΪ��ֵʱ��![]() �ǵ��������Σ�
�ǵ��������Σ�
��2���������OECQF�����Ϊ![]() ����ȷ��S��t�ĺ�����ϵʽ��
����ȷ��S��t�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ȫ��ͬ��������ֽƬABC��DEC�غϷ��ã�������C=900����B=��E=300.
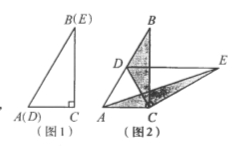


��1������������ͼ2���̶���ABC��ʹ��DEC�Ƶ�C��ת������Dǡ������BC����ʱ����գ��߶�DE��AC��λ�ù�ϵ�� ��
�� ����BDC�����ΪS1����AEC�����ΪS2����S1��S2��������ϵ�� ��
��2��������֤
����DEC�Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����S1��S2��������ϵ��Ȼ�����������Էֱ���������BDC����AEC��BC��CE���ϵĸߣ�����֤��С���IJ��롣
��3����չ̽��
��֪��ABC=600����D�����ƽ������һ�㣬BD=CD=4��OE��AB��BC�ڵ�E����ͼ4������������BA�ϴ��ڵ�F��ʹS��DCF =S��BDC,��ֱ��д����Ӧ��BF�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ���b2��4ac���ڷ���ax2+bx+c=0����������x1=��1��x2=3���۵�y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3���ܵ�x��0ʱ��y��x���������a��-![]() c���������������ȷ����_________������ţ�
c���������������ȷ����_________������ţ�
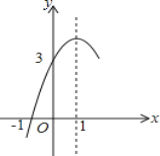
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
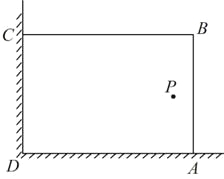
����Ŀ��������У�Ļ�У�ij��ȤС���������ͼ��ʾ��ֱ��ǽ�ǣ������㹻��������28m�������Χ��һ�����λ�ABCD�����ֻΧAB��BC���ߣ�����AB=xm.
��1�����������Ϊ192m2, ��x��ֵ��
��2������P����һ������ǽCD��AD�ľ���ֱ���15m��6m��Ҫ�������Χ�ڻ��ڣ����߽磬���������Ĵ�ϸ���������S�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ѧ�������ڶ�ʮ���й���������ѩ�����������⾰�۵��˽����,��ȫ��ѧ���������ȡ�˲���ѧ�����е���,���ѵ��������Ƴ���ͼ�IJ�����������ͳ��ͼ:
(1)���ε��鹲��ȡ�˶�����ѧ����
(2)ͨ�����㲹ȫ����ͼ��
(3)����ѧУ����![]() ��ѧ��,������Ƹ�ѧУѡ�����Ƚ��˽�����Ŀ��ѧ���ж�������
��ѧ��,������Ƹ�ѧУѡ�����Ƚ��˽�����Ŀ��ѧ���ж�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ĸ���������AB=BC���ڡ�ABC=90![]() ����AC=BD����AC��BD������ѡȡ������Ϊ����������ʹ��BCDΪ�����Σ���ͼ����������������ѡ�������д������ ( )
����AC=BD����AC��BD������ѡȡ������Ϊ����������ʹ��BCDΪ�����Σ���ͼ����������������ѡ�������д������ ( )
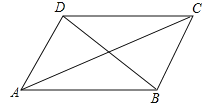
A. �ڢ� B. �ڢ� C. �٢� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
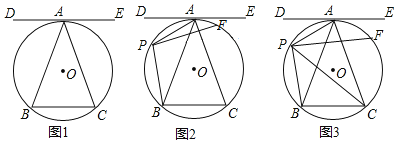
����Ŀ��.��ͼ����O����ABC�����Բ��ֱ��DE�ǡ�O�����ߣ���AΪ�е㣬DE��BC��
��1����ͼ1.��֤��AB=AC��
��2����ͼ2.��P�ǻ�AB��һ���㣬����PA��PB����PF��PB,����Ϊ��P,PF����O�ڵ�F, ��֤����BAC=2��APF��
��3����ͼ3.�ڣ�2���������£�����PC��PA=![]() ��PB=
��PB=![]() ��PC=
��PC=![]() �����߶�PF�ij�.
�����߶�PF�ij�.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com