
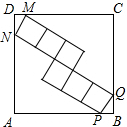
 在边长为10的正方形ABCD中,内接有6个大小相同的正方形,P、Q、M、N是落在大正方形边上的小正方形的顶点,如图所示,则这六个小正方形的面积是( )
在边长为10的正方形ABCD中,内接有6个大小相同的正方形,P、Q、M、N是落在大正方形边上的小正方形的顶点,如图所示,则这六个小正方形的面积是( )| A. | $\frac{134}{25}$ | B. | $\frac{408}{25}$ | C. | $\frac{816}{25}$ | D. | $\frac{{12\sqrt{34}}}{5}$ |
分析 如图,过点Q作QF⊥AD,垂足为F,可以得到△BQP∽△FQN,再根据相似三角形对应边成比例的性质列式求解即可得到QB和DN,根据勾股定理可求QN的长,从而求出六个小正方形的面积和.
解答 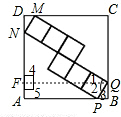 解:如图所示:
解:如图所示:
∵正方形ABCD边长为10,
∴∠A=∠B=90°,AB=10,
过点Q作QF⊥AD,垂足为F,则∠4=∠5=90°,
∴四边形AFQB是矩形,
∴∠2+∠3=90°,QF=AB=10,
∵六个大小完全一样的小正方形如图放置在大正方形中,
∴∠1+∠2=90°,
∴∠1=∠PQB,
∴△BQP∽△FQN,
∴$\frac{QB}{QF}$=$\frac{QP}{QN}$=$\frac{1}{5}$,
∴$\frac{QB}{10}$=$\frac{1}{5}$,
∴QB=2.
∴AF=2.
同理DN=2.
∴NF=AD-DN-AF=6.
∴QN=$\sqrt{Q{F}^{2}+F{N}^{2}}$=$\sqrt{1{0}^{2}+{6}^{2}}$=2$\sqrt{34}$,
∴小正方形的边长为$\frac{2\sqrt{34}}{5}$,
则六个小正方形的面积和是6×($\frac{2\sqrt{34}}{5}$)2=$\frac{816}{25}$.
故选C.
点评 本题考查了相似三角形的判定和性质,三角形的面积,等积变换,本题主要利用相似三角形的判定和相似三角形对应边成比例的性质和勾股定理,综合性较强,有一定的难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
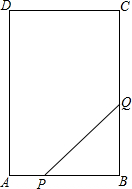 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB边向点B以1cm/s的速度运动,同时,点Q从点B出发沿BC边向点C以2cm/s的速度运动,P,Q两点在分别到达B,C两点后就停止运动,设经过ts时,△PBQ的面积为S cm2
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB边向点B以1cm/s的速度运动,同时,点Q从点B出发沿BC边向点C以2cm/s的速度运动,P,Q两点在分别到达B,C两点后就停止运动,设经过ts时,△PBQ的面积为S cm2查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com