
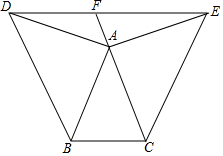
 如图,△ABC中,AB=AC,∠BAC=40°,分别以AB、AC为边在形外作两个等腰直角三角形ABD和等腰直角三角形ACE,使∠BAD=∠CAE=90°.连结DE,CA的延长线交DE于F.
如图,△ABC中,AB=AC,∠BAC=40°,分别以AB、AC为边在形外作两个等腰直角三角形ABD和等腰直角三角形ACE,使∠BAD=∠CAE=90°.连结DE,CA的延长线交DE于F.分析 (1)根据等腰三角形的性质及三角形内角和定理即可求得∠DBC的度数;
(2)证明△ABD≌△ACE即可得到结论.
(3)结论:△CEF不是等腰三角形.求出△ECF的内角即可判断;
解答 (1)解:∵△ABD为等腰直角三角形,
∴∠DBA=45°.
又∵AB=AC,∠BAC=40°,
∴∠ABC=70°.
∴∠DBC=115°;
(2)证明:∵△ABD和△ACE均为等腰直角三角形,
∴∠BAD=∠CAE=90°,AB=AD,AC=AE.
又∵AB=AC,
∴AB=AD=AC=AE.
∴△ABD≌△ACE.
∴BD=CE.
(3)结论:△CEF不是等腰三角形.
理由:∵∠DAE=360°-90°-90°-40°=140°,
∵AD=AE,
∴∠ADE=∠AED=20°,
∴∠CEF=∠AED+∠AEC=65°,
∴∠CFE=180°-45°-65°=70°,
∴∠CFE≠∠CEF,∠ECF≠∠CFE,∠ECF≠∠FEC,
∴△CEF不是等腰三角形.
点评 本题考查了全等三角形的判定、三角形的内角和定理、等腰三角形的判定;得到AB=AD=AC=AE是正确解答本题的关键.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
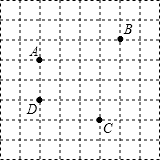 如图,已知A、B、C、D是网格纸上的四个格点,根据要求在网格中画图.
如图,已知A、B、C、D是网格纸上的四个格点,根据要求在网格中画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 |
| 摸出红球的频数 | 14 | 23 | 38 | 52 | 67 | 80 | 93 |
| 摸出红球的频率 | 35% | 28.75% | 32% | 33% | 33.55 | 33.33% | 33% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com