
 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G.F为AB边上一点,连接CF,且∠ACF=∠CBG.分析 (1)利用“ASA”判断△BCG≌△CFA,从而得到BG=CF;
(2)连结AG,利用等腰直角三角形的性质得CG垂直平分AB,则BG=AG,再证明∠D=∠GAD得到AG=DG,所以BG=DG,接着证明△ADE≌△CGE得到DE=GE,则BG=2DE,利用利用△BCG≌△CFA得到CF=BG,于是有CF=2DE;
(3)先得到BG=2,GE=1,则BE=3,设CE=x,则BC=AC=2CE=2x,在Rt△BCE中利用勾股定理得到x2+(2x)2=32,解得x=$\frac{3\sqrt{5}}{5}$,所以BC=$\frac{6\sqrt{5}}{5}$,AB=$\sqrt{2}$BC=$\frac{6\sqrt{10}}{5}$,然后在Rt△ABD中利用勾股定理计算AD的长.
解答 (1)证明:∵∠ACB=90°,AC=BC,
∴△ACB为等腰直角三角形,
∴∠CAF=∠ACG=45°,
∵CG平分∠ACB,
∴∠BCG=45°,
在△BCG和△CFA中
$\left\{\begin{array}{l}{∠CBG=∠ACF}\\{BC=CA}\\{∠BCG=∠CAF}\end{array}\right.$,
∴△BCG≌△CFA,
∴BG=CF;
(2)证明:连结AG,
∵CG为等腰直角三角形ACB的顶角的平分线,
∴CG垂直平分AB,
∴BG=AG,
∴∠GBA=∠GAB,
∵AD⊥AB,
∴∠D+∠DBA=90°,∠GAD+∠GAB=90°,
∴∠D=∠GAD,
∴AG=DG,
∴BG=DG,
∵CG⊥AB,DA⊥AB,
∴CG∥AD,
∴∠DAE=∠GCE,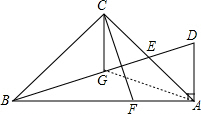
∵E为AC边的中点,
∴AE=CE,
在△ADE和△CGE中
$\left\{\begin{array}{l}{∠DAE=∠GCE}\\{AE=CE}\\{∠AED=∠CEG}\end{array}\right.$,
∴△ADE≌△CGE,
∴DE=GE,
∴DG=2DE,
∴BG=2DE,
∵△BCG≌△CFA,
∴CF=BG,
∴CF=2DE;
(3)解:∵DE=1,
∴BG=2,GE=1,即BE=3,
设CE=x,则BC=AC=2CE=2x,
在Rt△BCE中,x2+(2x)2=32,解得x=$\frac{3\sqrt{5}}{5}$,
∴BC=$\frac{6\sqrt{5}}{5}$,
∴AB=$\sqrt{2}$BC=$\frac{6\sqrt{10}}{5}$,
在Rt△ABD中,∵BD=4,AB=$\frac{6\sqrt{10}}{5}$,
∴AD=$\sqrt{{4}^{2}-(\frac{6\sqrt{10}}{5})^{2}}$=$\frac{2\sqrt{10}}{5}$.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.也考查了等腰直角三角形的性质.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
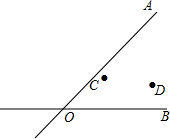 在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)
在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2016年全国中小学生“安全教育日”主题:“强化安全意识,提升安全素养”,小刚骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
2016年全国中小学生“安全教育日”主题:“强化安全意识,提升安全素养”,小刚骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y1=2x+2及直线y2=-x+5,.
已知直线y1=2x+2及直线y2=-x+5,.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com