
【题目】在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作DF⊥BC,交AB的延长线于E,垂足为F.
(1)如图①,求证直线DE是⊙O的切线; 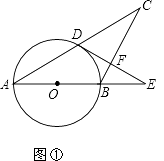
(2)如图②,作DG⊥AB于H,交⊙O于G,若AB=5,AC=8,求DG的长. 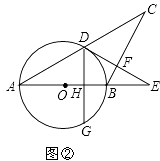
【答案】
(1)证明:连接OD,如图,

∵AB=BC,
∴∠A=∠C.
∵OA=OD,
∴∠A=∠ADO.
∴∠C=∠ADO.
∴OD∥BC.
∵DF⊥BC,
∴∠ODE=90°.
∴直线DE是⊙O的切线;
(2)解:连接DB,
∵AB是⊙O的直径,
∴∠ADB=90°.
∵AB=BC,
∴AD=DC.
∵AC=8,
∴AD=4.
在Rt△ADB中,BD= ![]() =
= ![]() =3,
=3,
∵DG⊥AB于H,
由三角形面积公式,得ABDH=ADDB.
∴DH= ![]() =
= ![]() ,
,
∵AB⊥DG,
∴DG=2DH= ![]()
【解析】(Ⅰ)连接OD,由AB=BC,OA=OD,得到∠A=∠C,∠A=∠ADO,则∠C=∠ADO,得到OD∥BC;而DF⊥BC,则∠ODE=90°,根据切线的判定定理即可得到结论;(Ⅱ)连接BD,AB是⊙O的直径,根据圆周角定理的推论得到∠ADB=90°.而AB=BC,则AD=DC=4.在Rt△ADB中,利用勾股定理可计算出BD=3,再利用等积法得到ABDH=ADDB,可计算出DH,然后根据垂径定理得到DG=2DH.
【考点精析】关于本题考查的勾股定理的概念和圆周角定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,对角线AC、BD交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BO于H.连接OG、CG.
(1)求证:AH=BE;
(2)试探究:∠AGO 的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面积.
,求△OGC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
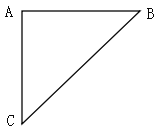
【题目】《九章算术》“勾股”章的问题::“今有二人同所立,甲行率七,乙行率三,乙东行,甲南行十步而斜东北与乙会.问甲、乙各行几何?”大意是说:如图,甲乙二人从A处同时出发,甲的速度与乙的速度之比为7:3,乙一直向东走,甲先向南走十步到达C处,后沿北偏东某方向走了一段距离后与乙在B处相遇,这时,甲乙各走了多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
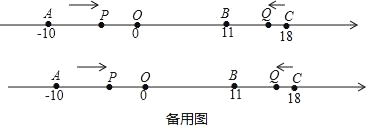
【题目】如图,在数轴上,点A表示﹣10,点B表示11,点C表示18.动点P从点A出发,沿数轴正方向以每秒2个单位的速度匀速运动;同时,动点Q从点C出发,沿数轴负方向以每秒1个单位的速度匀速运动.设运动时间为t秒.
(1)当t为何值时,P、Q两点相遇?相遇点M所对应的数是多少?
(2)在点Q出发后到达点B之前,求t为何值时,点P到点O的距离与点Q到点B的距离相等;
(3)在点P向右运动的过程中,N是AP的中点,在点P到达点C之前,求2CN﹣PC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2AB,E、F、G、H分别是AB,BC,CD,AD边上的点,EG⊥FH,FH=2 ![]() ,则四边形EFGH的面积为( )
,则四边形EFGH的面积为( ) 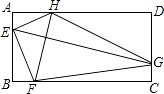
A.8 ![]()
B.8
C.12 ![]()
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点C在线段AB上,线段AC=10厘米,BC=6厘米,点M,N分别是AC,BC的中点.
![]()
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,求MN的长度;
(3)动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿AB向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批彩色弹力球的质量检验结果如下表:
抽取的彩色弹力球数n | 500 | 1000 | 1500 | 2000 | 2500 |
优等品频数m | 471 | 946 | 1426 | 1898 | 2370 |
优等品频率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
(1)请在图中完成这批彩色弹力球“优等品”频率的折线统计图
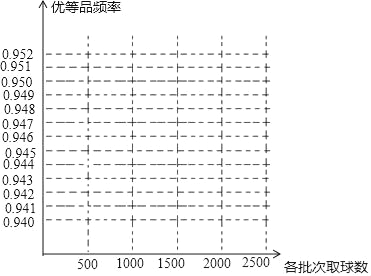
(2)这批彩色弹力球“优等品”概率的估计值大约是多少?(精确到0.01)
(3)从这批彩色弹力球中选择5个黄球、13个黑球、22个红球,它们除了颜色外都相同,将它们放入一个不透明的袋子中,求从袋子中摸出一个球是黄球的概率.
(4)现从第(3)问所说的袋子中取出若干个黑球,并放入相同数量的黄球,搅拌均匀,使从袋子中摸出一个黄球的概率为![]() ,求取出了多少个黑球?
,求取出了多少个黑球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com