练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．若两个三角形全等，猜想它们对应的高、中线、角平分线的关系是对应相等．

    分析 根据能够互相重合的两个三角形叫做全等三角形解答．

    解答 解：若两个三角形全等，则它们对应的高、中线、角平分线的关系是对应相等．
    故答案为：对应相等．

    点评 本题考查了全等三角形的性质，熟记性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．计算：
    ①$\sqrt{12}$÷$\sqrt{3}$+（$\sqrt{3}$+$\sqrt{2}$）（$\sqrt{3}$-$\sqrt{2}$）；      
    ②$\frac{sin60°}{cos30°}$-tan45°+cos245°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．把一个内径为8厘米，高为10厘米的圆柱形玻璃杯装满水，倒入一个内径为4厘米，高为48厘米的圆柱形容器中，倒完以后，容器中的水面离容器口有多少厘米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．a÷b×$\frac{1}{b}$=$\frac{a}{{b}^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

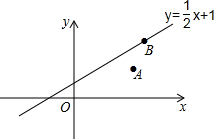    18．如图，B（6，4）在函数y=$\frac{1}{2}$x+1的图象上，A（5，2），点C在x轴上，点D在函数y=$\frac{1}{2}$x+1上，以A、B、C、D四个点为顶点构成平行四边形，写出所有满足条件的D点的坐标（2，2）或 D（-6，-2）、D（10，6）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，已知AB∥CD，EF⊥CD，若∠1=62°，则∠2的度数是28°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

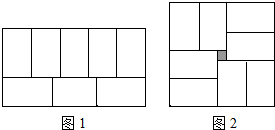    15．小明在拼图时发现，用8个一样大的长方形恰好可以拼成一个大的长方形，如图1所示；小红看见了，说：“我来试一试!”结果小红七拼八凑，拼成了一个如图2所示的正方形，但中间留下了一个洞，恰好是边长为2mm的小正方形．则每个小长方形的长是10mm，宽是6mm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图①，点O为直线AB上一点，过O点作射线OC，使∠BOC=120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方
    （1）将图①中的三角板绕点O按逆时针方向旋转至图②，使一边OM在∠BOC的内部，且恰好平分∠BOC．问：直线ON是否平分∠AOC？请说明理由．
    （2）将图①中的三角板绕点O按每秒6°的速度逆时针方向旋转一周，在旋转的过程中，直线ON恰好平分∠AOC，求旋转时间t的值．
    （3）将图①中的三角板绕点O按顺时针方向旋转至图③的位置，使ON在∠AOC的内部，请探究：∠AOM与∠NOC之间的数量关系，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图1，已知抛物线F1：y=x2-2x+2与y轴交于点A，顶点为B，抛物线F2：y=x2+ax+b的顶点为D在线段AB的延长线上（不包括B点），两抛物线相交于点C．
    （1）①若a=-4，求b的值；
    ②请用含a的式子表达b为b=$\frac{{a}^{2}+2a+8}{4}$；
    （2）如图1，若∠ACD=90°，求a的值；
    （3）如图2，若抛物线F2与直线AB另一个交点为E，连接CE，若△CDE的面积不小于3，求a的取值范围．

    查看答案和解析>>

    同步练习册答案