
����Ŀ����֪������y��x2��2mx+m2��2��y�ύ�ڵ�C��
��1�������ߵĶ�������Ϊ�� ������C����Ϊ�� �������ú�m�Ĵ���ʽ��ʾ��
��2����m��1ʱ������������һ����P����P�������Ϊn����n��0��
������P��x��ľ���Ϊ2ʱ�����P�����ꣻ
�����������ڵ�C���P֮�䲿�֣�����C�͵�P����ߵ�����͵�������֮��Ϊh����h��n֮��ĺ�����ϵʽ����д���Ա���n��ȡֵ��Χ��
��3������A����3��2����B��2��2��������AB����������y��x2��2mx+m2��2���߶�ABֻ��һ������ʱ��ֱ��д��m��ȡֵ��Χ��
���𰸡���1����m����2������0��m2��2������2����P1��1����2����P2��3��2������ ����3��m��ȡֵ��ΧΪ��5��m����1��0��m��4��
����3��m��ȡֵ��ΧΪ��5��m����1��0��m��4��
��������
��1����x��0ʱ�����y��ֵ������д����C���꣬��������y��x2��2mx+m2��2��Ϊ����ʽ����д���������ꣻ
��2���ٵ�m��1ʱ������������ߵĽ���ʽ���ٷֱ�y����2�������ʽ���������P���ꣻ
���ú�n�Ĵ���ʽ��ʾ����P�����꣬�ֵ�P��y����࣬��y���Ҳ����ڶԳ��������Ҳ�����������ۣ�ֱ�������ߵ�����͵��������֮��ɣ�
��3��������������ۣ���m��0�������߾����߶ε�����˵�![]() ʱ�����m��ֵ������ͼ����ͼ��m��ȡֵ��Χ����m��0�������߾����߶ε����Ҷ˵�B
ʱ�����m��ֵ������ͼ����ͼ��m��ȡֵ��Χ����m��0�������߾����߶ε����Ҷ˵�B![]() ʱ�����m��ֵ������ͼ����ͼ��m��ȡֵ��Χ��
ʱ�����m��ֵ������ͼ����ͼ��m��ȡֵ��Χ��
��1��y��x2��2mx+m2��2
����x��m��2��2��
�ඥ������Ϊ��m����2����
��y��x2��2mx+m2��2��
��x��0ʱ��y��m2��2��
���C������0��m2��2����
�ʴ�Ϊ����m����2������0��m2��2����
��2���ٵ�m��1ʱ��y��x2��2x��1��
��P��n��n2��2n��2����
��n2��2n��1����2��
��ã�n1��n2��1��
��P1��1����2����
��n2��2n��1��2��
��ã�n1��3��n2����1��n��0����ȥ����
��P2��3��2����
���ϣ�P1��1����2����P2��3��2����
����y��x2��2x��1�У��Գ���Ϊ![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
�ඥ������Ϊ![]() ��
��
�ߵ�P�ĺ�����Ϊn��
���P�ĺ�����Ϊ![]() ��
��

��ͼ������P��y����࣬��![]() ʱ��
ʱ��
![]() ��
��
����y���Ҳ����ڶԳ�����࣬��![]() ʱ��
ʱ��
![]() ��
��
���ڶԳ����Ҳ࣬��![]() ʱ��
ʱ��
![]() ��
��
���ϣ�
��3���ٵ�m��0�������߾����߶ε�����˵�A����3��2��ʱ��
����3��m��2��2��2��
��ã�m1����5��m2����1��
���Ӧ�����ߵ�ͼ����ͼ1��ͼ2��ʾ��


��ͼ����Կ�������5��m����1ʱ��������y��x2��2mx+m2��2���߶�ABֻ��һ�����㣻
�ڵ�m��0�������߾����߶ε����Ҷ˵�B��2��2��ʱ��
��2��m��2��2��2��
��ã�m1��4��m2��0��
���Ӧ�����ߵ�ͼ����ͼ3��ͼ4��ʾ��


��ͼ����Կ�����0��m��4ʱ��������y��x2��2mx+m2��2���߶�ABֻ��һ�����㣻
����������m��ȡֵ��ΧΪ��5��m����1��0��m��4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���ACB��45����BC��5��AC��2![]() ��D��BC���ϵĶ��㣬����AD�����߶�AD�Ƶ�A��ʱ����ת90���õ��߶�AE������EC��
��D��BC���ϵĶ��㣬����AD�����߶�AD�Ƶ�A��ʱ����ת90���õ��߶�AE������EC��
��1����ͼa����֤��CE��BC��
��2������ED��MΪAC���е㣬NΪED���е㣬����MN����ͼb��
��д��DE��AC��MN�����߶ε�������ϵ����˵�����ɣ�
���ڵ�D�˶��Ĺ����У���BD�ij�Ϊ��ֵʱ��M��E����֮��ľ�����С����Сֵ���� ������ֱ��д�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+3x+m-1=0������ʵ�����ֱ�Ϊx1,x2��
��1����m��ȡֵ��Χ��
��2����2��x1+x2��+ x1x2+10=0����m��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����κ���ͼ���ϲ��ֵ�ĺ�����![]() ��������
��������![]() �Ķ�Ӧֵ���±���ʾ��
�Ķ�Ӧֵ���±���ʾ��
| ... |
|
|
|
|
| ... |
| ... |
|
|
|
|
| ... |
��1����������κ����ı���ʽ��
��2���ڸ�����ƽ��ֱ������ϵ�л���������κ�����ͼ��

��3![]() ʱ��
ʱ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�����ABCD�ı�AB:BC��3:2����A��3��0����B��0��6���ֱ���x�ᣬy���ϣ�����������![]() (x��0)��ͼ����D����
(x��0)��ͼ����D����![]() ֵΪ�� ��
ֵΪ�� ��
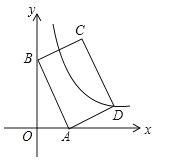
A. ��14 B. 14 C. 7 D. ��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���
�У���![]() ��y�ǹ���
��y�ǹ���![]() �Ķ��κ�����������
�Ķ��κ�����������![]() ������
������![]() .������
.������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() ������
������![]() �������жϣ�
�������жϣ�

�����������ߵĿ��ڷ�������£�
�ڵ�![]() ʱ�����������߱���ʽ�е�
ʱ�����������߱���ʽ�е�![]() ����
����![]() �����������
�����������
��������![]() �Ķ�����������
�Ķ�����������![]() ������Ϸ���
������Ϸ���
��������![]() ��
��![]() �ύ���ڵ�
�ύ���ڵ�![]() ���Ϸ�.
���Ϸ�.
������ȷ����
A.�٢ڢ�B.�٢ۢ�
C.�٢ڢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ڡ���![]() Ϊ�߶�
Ϊ�߶�![]() ������һ��.���ڸ�ƽ��������ĵ�
������һ��.���ڸ�ƽ��������ĵ�![]() ��������
��������![]() С�ڵ���
С�ڵ���![]() ��Ƶ�
��Ƶ�![]() Ϊ�߶�
Ϊ�߶�![]() ���������.
���������.
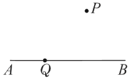
��1����ƽ��ֱ������ϵ![]() �У�����
������![]() .
.
���ڵĵ�![]() �У����߶�
�У����߶�![]() ������������� ��
������������� ��
�ڵ�P��ֱ��![]() ��һ�㣬����P���߶�AB������������������P������
��һ�㣬����P���߶�AB������������������P������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() .��ֱ��
.��ֱ��![]() �ϴ����߶�AB�������������ֱ��д��
�ϴ����߶�AB�������������ֱ��д��![]() ��ȡֵ��Χ
��ȡֵ��Χ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ������
������![]() ����
����![]() ���ڵ�
���ڵ�![]() .
.
��1���������ߵĽ���ʽ.
��2����![]() ���߶�
���߶�![]() ��һ���㣬����
��һ���㣬����![]() ��
��![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() �����������ڵ�
�����������ڵ�![]() �����߶�
�����߶�![]() �ij������ֵ.
�ij������ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�ķ��̣�x��4����x2��6x+m����0��������ǡ�ÿ������ijֱ�������ε����߳�����m��ֵΪ_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com