
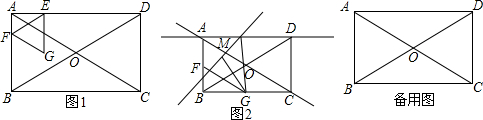
分析 (1)当G在BC边上时,如图1中,首先证明四边形ABGE是矩形,根据EF=EG=AB=2t,列出方程即可解决问题.
(2)分四种情形①如图2中,当0<t≤2时,重叠部分是四边形FGMN.②如图3中,当2<t≤4时,重叠部分是五边形MNFPK.③如图4中,当4<t≤$\frac{16}{3}$时,重叠部分是五边形OMKPE.④如图5中,当$\frac{16}{3}$<t≤6时,重叠部分是四边形OMGF.分别求解即可.
(3)分四种情形)①如图6中,当点N在AD上,点M在上时,易知∠MAN=∠ANM=30°,AM=MN,△AMN是以MN为腰的等腰三角形.②如图7中,当MN=NA时,连接CN.③如图8中,当MN=AN时,④如图9中,当AM=MN时,分别求解即可.
解答 解:(1)当G在BC边上时,如图1中,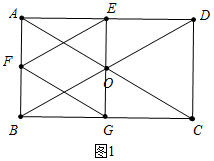
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AB=4,AD=4$\sqrt{3}$,
∴tan∠ABD=$\frac{AD}{AB}$=$\sqrt{3}$,
∴∠ABD=60°,
∵AE=$\sqrt{3}$t,AF=t,
∴tan∠AFE=$\frac{AE}{AF}$=$\sqrt{3}$,
∴∠AFE=60°,
∴∠AEF=30°,
∵△EFG是等边三角形,
∴EF=EG=FG,∠FEG=60°,
∴∠AEG=90°,
∵∠ABC=∠BAE=∠AEG=90°,
∴四边形ABGE是矩形,
∴EF=EG=AB,
∴2t=4
∴t=2.
(2 )①如图2中,当0<t≤2时,重叠部分是四边形FGMN.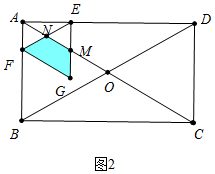
s=S△EFG-S△EMN=$\frac{\sqrt{3}}{4}$•(2t)2-$\frac{\sqrt{3}}{4}$•t2=$\frac{3\sqrt{3}}{4}$t2.
②如图3中,当2<t≤4时,重叠部分是五边形MNFPK.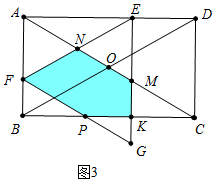
s═S△EFG-S△EMN-S△PKG=$\frac{\sqrt{3}}{4}$•(2t)2-$\frac{\sqrt{3}}{4}$•t2-$\frac{1}{2}$(2t-4)•$\sqrt{3}$(2t-4)=-$\frac{3\sqrt{3}}{4}$t2+8$\sqrt{3}$t-8$\sqrt{3}$.
③如图4中,当4<t≤$\frac{16}{3}$时,重叠部分是五边形OMKPE.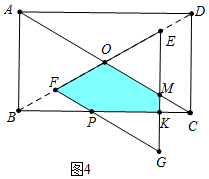
S=S△EFG-S△EOM-S△PKG=$\frac{\sqrt{3}}{4}$•[8-4(t-4)]2-$\frac{\sqrt{3}}{4}$•[4-2(t-4)]2-$\frac{1}{2}$(16-3t)•$\sqrt{3}$(16-3t)=-$\frac{3\sqrt{3}}{2}$t2+12$\sqrt{3}$t-45$\sqrt{4}$.
④如图5中,当$\frac{16}{3}$<t≤6时,重叠部分是四边形OMGF.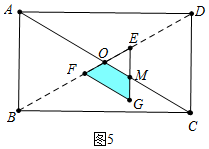
S=S△EFG-S△EOM=$\frac{\sqrt{3}}{4}$•[8-4(t-4)]2-$\frac{\sqrt{3}}{4}$•[4-2(t-4)]2=3$\sqrt{3}$t2-36$\sqrt{3}$t+108$\sqrt{3}$.
综上所述,S=$\left\{\begin{array}{l}{\frac{3\sqrt{3}}{4}{t}^{2}}&{(0<t≤2)}\\{-\frac{3\sqrt{3}}{4}{t}^{2}+8\sqrt{3}t-8\sqrt{3}}&{(2<t≤4)}\\{-\frac{3\sqrt{3}}{2}{t}^{2}+12\sqrt{3}t-45\sqrt{3}}&{(4<t≤\frac{16}{3})}\\{3\sqrt{3}{t}^{2}-36\sqrt{3}t+108\sqrt{3}}&{(\frac{16}{3}<t≤6)}\end{array}\right.$.
(3)存在,理由如下:
①如图6中,当点N在AD上,点M在上时,易知∠MAN=∠ANM=30°,AM=MN,△AMN是以MN为腰的等腰三角形.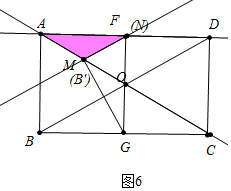
此时,∵AN=2$\sqrt{3}$,作MH⊥AF于H,
∴AH=NH=$\sqrt{3}$,cos30°=$\frac{AH}{AM}$,
∴$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{AM}$,
∴AM=2cm.
②如图7中,当MN=NA时,连接CN.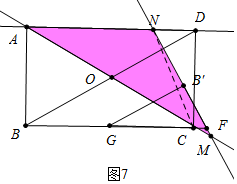
∵NA=NM,
∴∠NAM=∠NMA=30°,
∵∠FCM=∠FMC=30°,CF=4-2$\sqrt{3}$,
∴CM=2•CF•cos30°=4$\sqrt{3}$-6,
∴AM=AC+CM=(4$\sqrt{3}$+2)cm.
③如图8中,当MN=AN时,
易知O、G、F共线,△OFM是等边三角形,OM=6,
∴OM=OA+OM=4+6=10cm
④如图9中,当AM=MN时,作FH⊥DM于H,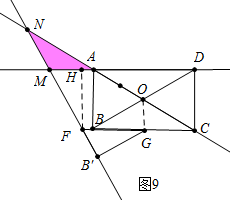
∵四边形ABFH是矩形,
∴AH=FB=4-2$\sqrt{3}$,
在Rt△FHM中,MH=$\frac{\sqrt{3}}{3}$FH=$\frac{4\sqrt{3}}{3}$,
∴AM=MH+AH=(4-$\frac{2\sqrt{3}}{3}$)cm.
综上所述,当△AMN是以MN为腰的等腰三角形时,AM的长为2cm或(4$\sqrt{3}$+2)cm或10cm或(4-$\frac{2\sqrt{3}}{3}$)cm.
点评 本题考查四边形综合题、旋转变换、矩形的性质、等腰三角形的性质和判定、锐角三角函数等知识,解题的关键是灵活运用所学知识,学会画正确图形,学会分类讨论,学会用分段函数表示函数关系式,本题体现了数形结合的数学思想,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
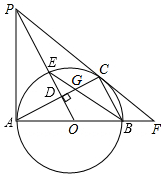 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P.连接BE交AC于G,连接PC并延长AB的延长线交于点F,BF=3,CF=4.
如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D,过点A作⊙O的切线AP,AP与OD的延长线交于点P.连接BE交AC于G,连接PC并延长AB的延长线交于点F,BF=3,CF=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
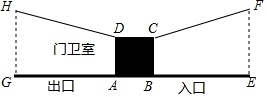 如图,这是一传媒公司寓意为“大鹏展翅”的大门建筑截面图,它是两条关于顶点成中心对称的抛物线,开口朝向左右,顶点为边长为4米的正方形中心,且分别过正方形的两个顶点.若入口水平宽BE为10.5米,则最高点F到地面的高度FE为7米.
如图,这是一传媒公司寓意为“大鹏展翅”的大门建筑截面图,它是两条关于顶点成中心对称的抛物线,开口朝向左右,顶点为边长为4米的正方形中心,且分别过正方形的两个顶点.若入口水平宽BE为10.5米,则最高点F到地面的高度FE为7米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com