Question

1．如图，Rt△ABC中，AB=AC=$4\sqrt{2}$，一动点P从B出发，沿BC方向以每秒1个单位长度的速度匀速运动，到达点C即停止，在整个运动过程中，过点P作PD⊥BC与Rt△ABC的直角边相交于点D，延长PD至点Q，使PD=QD，以PQ为斜边在PQ左侧作等腰直角三角形PQE．设运动时间为t秒．

（1）在整个运动过程中，当线段QE与线段AB在一条直线上时，求t的值；
（2）在整个运动过程中，设△ABC与△PQE重叠部分的面积为S，请直接写出S与t的函数关系式以及自变量t的取值范围；
（3）在整个运动过程中，连接AQ、AP，是否存在t值，使△APQ成为等腰三角形？若存在，求出t的值；若不存在，请说明理由．
（4）当t=4秒时，以PQ为斜边再在PQ右侧作等腰直角三角形PQF，将四边形PEQF绕点P旋转，PE与线段AB交于点M，PF与线段AC交于点N，在这一旋转过程中，试判断PM+FN的值是否发生变化？若发生变化，请直接写出变化的范围；若不发生变化，请直接写出此定值．

Answer 1

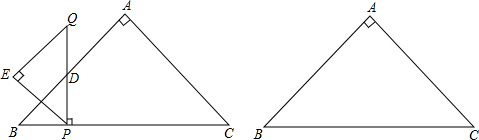
分析 （1）设BP=t，当线段QE与线段AB在一条直线上，根据相似三角形的判定和性质进行解答；
（2）当PQ过A时求出t=4，当E在AB上时求出t=$\frac{16}{3}$，当P到C点时t=8，即分为三种情况：根据三角形面积公式求出当0＜t≤4时，S=$\frac{1}{4}$t²，当4＜t≤$\frac{16}{3}$时，S=-$\frac{3}{4}$t²+8t-16，当$\frac{16}{3}$＜t＜8时，S=$\frac{3}{4}$t²-12t+48；
（3）存在，当点D在线段AB上时，求出QD=PD=t，PD=2t，过点A作AH⊥BC于点H，PH=BH-BP=4-t，在Rt△APH中求出AP=$\sqrt{A{H}^{2}+P{H}^{2}}$，（ⅰ）若AP=PQ，则有$\sqrt{{t}^{2}-8t+32}$=2t，（ⅱ）若AQ=PQ，过点Q作QG⊥AP于点G，根据△PGQ∽△AHP求出PG=$\frac{8t}{\sqrt{{t}^{2}-8t+32}}$，若AQ=PQ，得出$\frac{8t}{\sqrt{{t}^{2}-8t+32}}=\frac{1}{2}\sqrt{{t}^{2}-8t+32}$．（ⅲ）若AP=AQ，过点A作AT⊥PQ于点T，得出4=$\frac{1}{2}$×2t，求出方程的解即可；
（4）四边形PMAN的面积不发生变化，连接AP，此时t=4秒，求出S_{四边形PMAN}=S_△APM+S_△APN=S_△CPN+S_△APN=S_△ACP=$\frac{1}{2}$×CP×AP=8．

解答 解：（1）设BP=t，当线段QE与线段AB在一条直线上时，如图a，
可得：PC=8-t，
所以：DC=$\sqrt{2}（8-t）$，
∵∠ADQ=∠PDC，∠DAQ=∠DPC，
∴△ADQ～△PDC，
∴$\frac{DA}{DP}=\frac{DQ}{DC}$，
∵DQ=PD，
即：$\frac{DA}{DP}=\frac{PD}{DC}$，
即：$\frac{4\sqrt{2}-\sqrt{2}（8-t）}{8-t}=\frac{8-t}{\sqrt{2}（8-t）}$，
解得：t=$\frac{16}{3}$；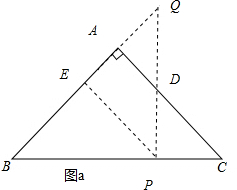

（2）当0＜t≤4时，S=$\frac{1}{4}$t²，
当4＜t≤$\frac{16}{3}$时，S=-$\frac{3}{4}$t²+8t-16，
当$\frac{16}{3}$＜t＜8时，S=$\frac{3}{4}$t²-12t+48；
（3）存在，理由如下：
当点D在线段AB上时，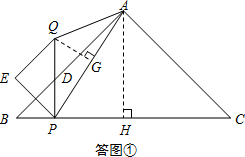
∵AB=AC，
∴∠B=∠C=$\frac{1}{2}$（180°-∠BAC）=45°．
∵PD⊥BC，
∴∠BPD=90°，
∴∠BDP=45°，
∴PD=BP=t，
∴QD=PD=t，
∴PQ=QD+PD=2t．
过点A作AH⊥BC于点H，
∵AB=AC，
∴BH=CH=$\frac{1}{2}$BC=4，AH=BH=4，
∴PH=BH-BP=4-t，
在Rt△APH中，AP=$\sqrt{A{H}^{2}+P{H}^{2}}$；
（ⅰ）若AP=PQ，则有$\sqrt{{t}^{2}-8t+32}$=2t．
解得：t₁=$\frac{4\sqrt{7}-4}{3}$，t₂=$\frac{-4\sqrt{7}-4}{3}$（不合题意，舍去）；
（ⅱ）若AQ=PQ，过点Q作QG⊥AP于点G，如图（1），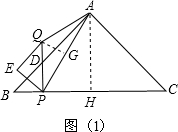
∵∠BPQ=∠BHA=90°，
∴PQ∥AH．
∴∠APQ=∠PAH．
∵QG⊥AP，
∴∠PGQ=90°，
∴∠PGQ=∠AHP=90°，
∴△PGQ∽△AHP，
∴$\frac{PG}{AH}=\frac{PQ}{AP}$，即$\frac{PG}{4}=\frac{2t}{\sqrt{{t}^{2}-8t+32}}$，
∴PG=$\frac{8t}{\sqrt{{t}^{2}-8t+32}}$，
若AQ=PQ，由于QG⊥AP，则有AG=PG，即PG=$\frac{1}{2}$AP，
即$\frac{8t}{\sqrt{{t}^{2}-8t+32}}=\frac{1}{2}\sqrt{{t}^{2}-8t+32}$．
解得：t₁=12-$4\sqrt{7}$，t₂=12+$4\sqrt{7}$（不合题意，舍去）；
（ⅲ）若AP=AQ，过点A作AT⊥PQ于点T，如图（2），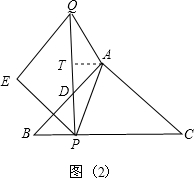
易知四边形AHPT是矩形，故PT=AH=4．
若AP=AQ，由于AT⊥PQ，则有QT=PT，即PT=$\frac{1}{2}$PQ，
即4=$\frac{1}{2}$×2t．解得t=4．
当t=4时，A、P、Q三点共线，△APQ不存在，故t=4舍去．
综上所述，存在这样的t，使得△APQ成为等腰三角形，即t₁=$\frac{4\sqrt{7}-4}{3}$秒或t₂=（12-$4\sqrt{7}$）秒；
（4）四边形PMAN的面积不发生变化．理由如下：
∵等腰直角三角形PQE，
∴∠EPQ=45°，
∵等腰直角三角形PQF，
∴∠FPQ=45°．
∴∠EPF=∠EPQ+∠FPQ=45°+45°=90°，
连接AP，如图（3），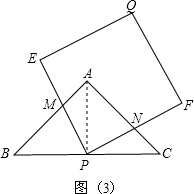
∵此时t=4秒，
∴BP=4×1=4=$\frac{1}{2}$BC，
∴点P为BC的中点．
∵△ABC是等腰直角三角形，
∴AP⊥BC，AP=$\frac{1}{2}$BC=CP=BP=4，∠BAP=∠CAP=$\frac{1}{2}$∠BAC=45°，
∴∠APC=90°，∠C=45°，
∴∠C=∠BAP=45°，
∵∠APC=∠CPN+∠APN=90°，
∠EPF=∠APM+∠APN=90°，
∴∠CPN=∠APM，
∴△CPN≌△APM，
∴S_△CPN=S_△APM，
∴S_{四边形PMAN}=S_△APM+S_△APN=S_△CPN+S_△APN=S_△ACP=$\frac{1}{2}$×CP×AP=$\frac{1}{2}$×4×4=8．
∴四边形PMAN的面积不发生变化，此定值为8．

点评 本题考查了三角形面积，相似三角形的性质和判定，三角形内角和定理，等腰直角三角形等知识点的综合运用，用了分类讨论思想和方程思想，难度偏大．