Question

16．如图所示，在△ABC中，AB=AC，点O为△ABC的外心，点D是AB的中点，点E是△ACD的重心，求证：OE⊥CD．

Answer 1

分析 如图，延长AO交BC于M，J交CD于G，延长DE交AC于F，连接FM、EG，首先证明EG∥FM∥AB，再证明G是△ODE的垂心即可．

解答 证明：如图，延长AO交BC于M，J交CD于G，延长DE交AC于F，连接FM、EG．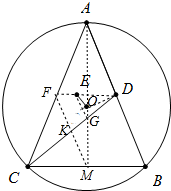

∵AB=AC，O是外心，
∴AM⊥BC，CM=BM，
∵E是重心，
∴EF：DE=1：2，
∵AM、CD是中线，
∴G是△ABC的重心，
∴GD：GC=1：2，
∵FM∥AB，FM=$\frac{1}{2}$AB，
∴CK=KD，
∴DG：GK=$\frac{1}{3}$CD：（$\frac{1}{2}$CD-$\frac{1}{3}$CD）=2：1，
∴DE：EF=DG：GK，
∴EG∥FK，
∵OD⊥AB，EG∥FM∥AB，
∴EG⊥OD，
∵DF∥BC，AM⊥BC，
∴OE⊥ED，
∴点G是△ODE的垂心，
∴EO⊥DG，即OE⊥CD．

点评 本题考查三角形外接圆与外心、三角形的重心、等腰三角形的性质、平行线的判定、垂心等知识，解题的关键是学会添加辅助线，想到证明G是△ODE的垂心是解题的突破口，题目有难度，辅助线比较多．