
【题目】把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG. 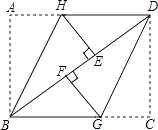
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,∠A=∠C=90°,∠ABD=∠BDC,
∵△BEH是△BAH翻折而成,
∴∠ABH=∠EBH,∠A=∠HEB=90°,AB=BE,
∵△DGF是△DGC翻折而成,
∴∠FDG=∠CDG,∠C=∠DFG=90°,CD=DF,
∴∠DBH= ![]() ∠ABD,∠BDG=
∠ABD,∠BDG= ![]() ∠BDC,
∠BDC,
∴∠DBH=∠BDG,
∴△BEH与△DFG中,
∠HEB=∠DFG,BE=DF,∠DBH=∠BDG,
∴△BEH≌△DFG
(2)解:∵四边形ABCD是矩形,AB=6cm,BC=8cm,
∴AB=CD=6cm,AD=BC=8cm,
∴BD= ![]() =
= ![]() =10,
=10,
∵由(1)知,FD=CD,CG=FG,
∴BF=10﹣6=4cm,
设FG=x,则BG=8﹣x,
在Rt△BGF中,
BG2=BF2+FG2,即(8﹣x)2=42+x2,解得x=3,即FG=3cm
【解析】(1)先根据矩形的性质得出∠ABD=∠BDC,再由图形折叠的性质得出∠ABH=∠EBH,∠FDG=∠CDG,∠A=∠HEB=90°,∠C=∠DFG=90°,进而可得出△BEH≌△DFG;(2)先根据勾股定理得出BD的长,进而得出BF的长,由图形翻折变换的性质得出CG=FG,设FG=x,则BG=8﹣x,再利用勾股定理即可求出x的值.
【考点精析】本题主要考查了勾股定理的概念和矩形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
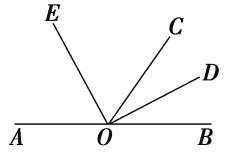
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1) -26-(-15) (2)(+7)+(-4)-(-3)-14
(3)(-3)×![]() ÷(-2)×(-
÷(-2)×(-![]() ) (4)-(3-5)+32×(-3)
) (4)-(3-5)+32×(-3)
(5)(﹣![]() +
+![]() ﹣
﹣![]() +
+![]() )÷
)÷![]() (6)- 32 -(﹣2)2+1.
(6)- 32 -(﹣2)2+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( ) 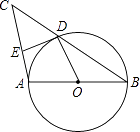
A.DE=DO
B.AB=AC
C.CD=DB
D.AC∥OD
查看答案和解析>>
科目:初中数学 来源: 题型:
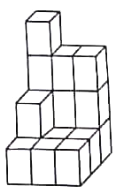
【题目】如图,在一次数学活动课上,张明用17个底面为正方形,且底面边长为![]() ,高为
,高为![]() 的小长方体达成了一个几何体,然后他请王亮用尽可能少的同样的长方体在旁边再搭一个几何体,使王亮所搭的几何体恰好可以和张明所搭的几何体拼成一个大长方体(即拼大长方体时将其中一个几何体翻转,且假定组成每个几何体的小长方体粘合在一起).
的小长方体达成了一个几何体,然后他请王亮用尽可能少的同样的长方体在旁边再搭一个几何体,使王亮所搭的几何体恰好可以和张明所搭的几何体拼成一个大长方体(即拼大长方体时将其中一个几何体翻转,且假定组成每个几何体的小长方体粘合在一起).
(1)王亮至少还需要 个小长方体;
(2)请画出张明所搭几何体的左视图,并计算它的表面积(用含![]() 的代数式表示);
的代数式表示);
(3)请计算(1)条件下王亮所搭几何体的表面积(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
![]() 求收工时,检修小组在
求收工时,检修小组在![]() 地的哪个方向?距离
地的哪个方向?距离![]() 地多远?
地多远?
![]() 在第几次纪录时距
在第几次纪录时距![]() 地最远?
地最远?
![]() 若汽车行驶每千米耗油
若汽车行驶每千米耗油![]() 升,问从
升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某动物园成人票每张20元,学生票每张5元,国庆期间特推出以下两种优惠方案:
方案一:购买一张成人票赠送一张学生票;
方法二:按总价的90%付款.
某校有4名教师带领若干名(不少于4人)学生去参观该动物园.
(1)设学生人数为x(人),付款总金额y(元),分别建立两种优惠方案中y与x的函数关系式;
(2)请计算并确定出比较节省费用的购票方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx﹣k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx﹣k的值大于函数y=x的值的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 “囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
(1)用含有x、y的代数式表示右图中“囧”的面积;
(2)当![]() 时,求此时“囧”的面积.
时,求此时“囧”的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com