
分析 (1)设每轮传染中平均一人传染x人,那么经过第一轮传染后有x人被感染,那么经过两轮传染后有x(x+1)+x+1人感染,又知经过两轮传染共有81人被感染,以经过两轮传染后被传染的人数相等的等量关系,列出方程求解;
(2)利用(1)中所求得出三轮感染后,患病的人数即可.
解答 解:(1)设每轮传染中平均一人传染x人,则第一轮后有x+1人感染,第二轮后有x(x+1)+x+1人感染,
由题意得:x(x+1)+x+1=81,
即:x1=8,x2=-10(不符合题意舍去).
所以,每轮平均一人传染8人.
(2)三轮感染后的人数为:81+81×8=729.
∵729>700,
∴3轮感染后,被感染的人数会超过700人.
点评 本题主要考查了一元二次方程的应用,关键在于理解清楚题意,找出等量关系列出方程求解,本题应注意是经过两轮传染后感染的总人数,而不仅仅只是第二轮被传染的人数.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
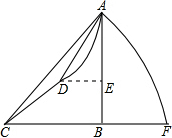 小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$.
小明在山脚C处测得山顶A的仰角为45°,他沿坡角为37°的斜坡前进200米到达D处,测得山顶A的仰角为53°,求山高AB(A、B、C、D、E、F在一个平面内)参考数据:sin37°=cos53°≈$\frac{3}{5}$,cos37°=sin53°≈$\frac{4}{5}$,tan53°≈$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com