
【题目】某新型高科技商品,每件的售价比进价多6元,5件的进价相当于4件的售价,每天可售出200件,经市场调查发现,如果每件商品涨价1元,每天就会少卖5件.
(1)该商品的售价和进价分别是多少元?
(2)设每天的销售利润为w元,每件商品涨价x元,则当售价为多少元时,该商品每天的销售利润最大,最大利润为多少元?
(3)为增加销售利润,营销部推出了以下两种销售方案:方案一:每件商品涨价不超过8元;方案二:每件商品的利润至少为24元,请比较哪种方案的销售利润更高,并说明理由.
【答案】(1)商品的售价30元,进价为24元.(2)售价为47元时,商品的销售利润最大,最大为2645元.(3)方案二的销售利润最高.
【解析】
(1)根据题目,设出未知数,列出二元一次方程组即可解答;
(2)根据题目:利润=每件利润×销售数量,列出二次函数,根据二次函数的最值问题,即可求出最大利润;
(3)分别根据两种方案,算出他们的最大利润,然后进行比较.
(1)该商品的售价x元,进价为y元,由题意得:
![]() ,解得
,解得![]() ,
,
故商品的售价30元,进价为24元.
(2)由题意得:w=(30+x-24)(200-5x)=-5(x-17)2+2645,
当每件商品涨价17元,即售价30+17=47元时,商品的销售利润最大,最大为2645元.
(3)方案一:每件商品涨价不超过8元,a=-5<0,
故当x=8时,利润最大,最大利润为w=-5(8-17)2+2645=2240元;
方案二:每件商品的利润至少为24元,即每件的售价应涨价:30+x-24≥24,解得x≥18,a=-5<0,
故当x=18时,利润最大,最大利润为w=-5(18-17)2+2645=2640元.
∵2640>2240,
∴方案二的销售利润最高.


科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地在一直线上,且相距
两地在一直线上,且相距![]() ,甲、乙两人同时从
,甲、乙两人同时从![]() 、
、![]() 出发,分别沿射线
出发,分别沿射线![]() 、
、![]() 行进,其中甲的速度为
行进,其中甲的速度为![]() ,设他们出发
,设他们出发![]() 时,甲、乙两人离
时,甲、乙两人离![]() 地的距离分别为
地的距离分别为![]() 、
、![]() ,
,![]() 与
与![]() 的部分函数图象如图所示:
的部分函数图象如图所示:

(1)分别写出![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在所给的平面直角坐标系中画出(1)中的函数图象,直接写出![]() 、
、![]() 的图象交点坐标并解释其实际意义.
的图象交点坐标并解释其实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某工程队在工地上利用互相垂直的两墙AE、AF,另两边用铁栅栏围成一个长方形场地ABCD,中间再用栅栏分割成两个长方形.铁栅栏总长180米,已知墙AE长90米,墙AF长60米.
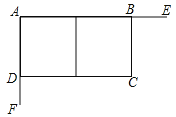
(1)设BC长为x米,长方形ABCD的面积为y,请写出y与x的函数关系,并写出x的取值范围;
(2)当BC的值为多少时,长方形ABCD的面积最大?
(3)若长方形ABCD的面积不能小于4000,请直接写出BC边长x(米)的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程 x2﹣(2k+1)x+4(k﹣![]() )=0.若等腰三角形ABC的一边长a=4,另两边边长b、c恰好是这个方程的两个实数根,则△ABC的周长为_____.
)=0.若等腰三角形ABC的一边长a=4,另两边边长b、c恰好是这个方程的两个实数根,则△ABC的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
(1)求AD的长;
(2)求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
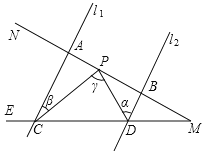
【题目】如图,已知l1∥l2,射线MN分别和直线l1,l2交于A、B,射线ME分别和直线l1,l2交于C、D,点P在A、B间运动(P与A、B两点不重合),设∠PDB=α,∠PCA=β,∠CPD=γ.
(1)试探索α,β,γ之间有何数量关系?说明理由.
(2)如果BD=3,AB=9,AC=6,并且AC垂直于MN,那么点P运动到什么位置时,△ACP≌△BPD说明理由.
(3)在(2)的条件下,当△ACP≌△BPD时,PC与PD之间有何位置关系,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com