
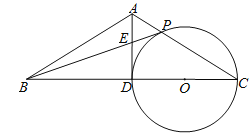
【题目】已知:如图,在△ABC中,AB=AC,点D是边BC的中点,以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
(1)求证:AD是⊙O的切线;
(2)如果PB是⊙O的切线,BC=4,求PE的长.
【答案】(1) 证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由AB=AC,点D是BC的中点可得AD⊥BC,结合CD是⊙O的直径,即可得AD是⊙O的切线;
(2)连接OP,由已知易求得BD、OB、OP和BP的长,再证PE=DE,△BDE∽△BPO即可列出比例式求得DE的长,从而可得PE的长.
试题解析:
(1)∵AB=AC,点D是边BC的中点,
∴AD⊥CD,
∵CD为⊙O的直径,
∴AD是⊙O的切线;
(2)连接OP,
∵点D是边BC的中点,BC=4,CD是⊙O的直径,
∴CD=BD=2,OP=1,OB=3,
∴在Rt△BOP中,BP=![]() ,
,
∵AD是⊙O的切线,PB是⊙O的切线,
∴PE=DE,∠BPO=90°,
∵AD⊥CD,
∴∠ADB=∠BPO=90°,
又∵∠DBE=∠PBO,
∴△BDE∽△BPO,
∴![]() ,即
,即![]() ,解得:DE=
,解得:DE=![]() ,
,
∴PE=DE=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过A(2,0),B(0,-6)两点.
的图象经过A(2,0),B(0,-6)两点.
(1)求这个二次函数的解析式及顶点坐标;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
(3)在抛物线的对称轴上是否存在一点P.使得以O、B、C、P四点为顶点的四边形是平行四边形?若存在,请直接写出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于F,OE⊥OB交BC边于点E.
(1)求证:△ABF∽△COE;
(2)当O为AC边中点, ![]() 时,如图2,求
时,如图2,求![]() 的值;
的值;
(3)当O为AC边中点, ![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区规划在一个长34m、宽22m的矩形ABCD上,修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为100m2,那么通道的宽应设计成____m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC,BD于点E,P,连接OE,∠ADC=60°,![]() ,则下列结论:①∠CAD=30°②
,则下列结论:①∠CAD=30°②![]() ③
③![]() ④
④![]() ,正确的个数是______________
,正确的个数是______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD和Rt△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.
(1)在图中画出点O和△CDF;
(2)若∠ABC=130°,直接写出∠AEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:

(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,可求得∠P的度数是 ;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,请直接写出∠P与∠D、∠B之间存在的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潜山市某村办工厂,今年前5个月生产某种产品的总量C(件)关于时间t(月)的函数图象如图所示,则该厂对这种产品来说( )

A. 1月至3月每月生产总量逐月增加,4、5两月每月生产总量逐月减少
B. 1月至3月每月生产总量逐月增加,4,5两月每月生产量与3月持平
C. 1月至3月每月生产总量逐月增加,4、5两月均停止生产
D. 1月至3月每月生产总量不变,4、5两月均停止生产
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com