
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
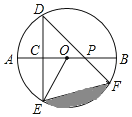
【答案】(1)![]() ;(2)
;(2)![]() π﹣
π﹣![]() .
.
【解析】
(1)根据垂径定理得CE的长,再根据已知DE平分AO得CO=![]() AO=
AO=![]() OE,根据勾股定理列方程求解.
OE,根据勾股定理列方程求解.
(2)先求出扇形的圆心角,再根据扇形面积和三角形的面积公式计算即可.
解:(1)连接OF,
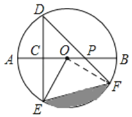
∵直径AB⊥DE,
∴CE=![]() DE=1.
DE=1.
∵DE平分AO,
∴CO=![]() AO=
AO=![]() OE.
OE.
设CO=x,则OE=2x.
由勾股定理得:12+x2=(2x)2.
x=![]() .
.
∴OE=2x=![]() .
.
即⊙O的半径为![]() .
.
(2)在Rt△DCP中,
∵∠DPC=45°,
∴∠D=90°﹣45°=45°.
∴∠EOF=2∠D=90°.
∴S扇形OEF=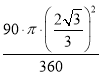 =
=![]() π.
π.
∵∠EOF=2∠D=90°,OE=OF=![]()
SRt△OEF=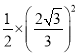 =
=![]() .
.
∴S阴影=S扇形OEF﹣SRt△OEF=![]() π﹣
π﹣![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E是矩形ABCD的边BC上一点,EF⊥AE,分别交AC,CD于点M,F,BG⊥AC,垂足为G,BG交AE于点H.
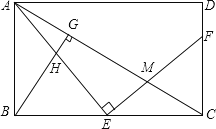
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC中点,BC=2AB,AB=4,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.


(1)求证:AE=![]() NE+ME;
NE+ME;
(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.猜想CH与FH存在的数量关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转![]() 角(0°<
角(0°<![]() <90°)得到△DEC,设CD交AB于点F,连接AD,当旋转角
<90°)得到△DEC,设CD交AB于点F,连接AD,当旋转角![]() 度数为________,△ADF是等腰三角形.
度数为________,△ADF是等腰三角形.
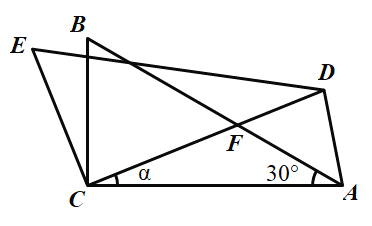
A.20°B.40°C.10°D.20°或40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代第一部数学专著,它的出现标志中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( )
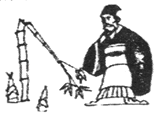
A.3B.5C.4.2D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
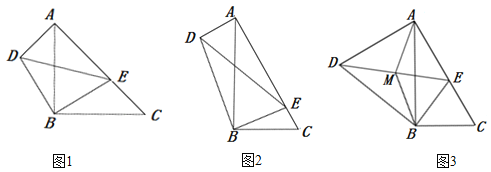
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=45°,点E是线段AC上一动点,连接DE.
填空:①则![]() 的值为______;②∠EAD的度数为_______.
的值为______;②∠EAD的度数为_______.
(2)类比探究
如图2,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=60°,点E是线段AC上一动点,连接DE.请求出![]() 的值及∠EAD的度数;
的值及∠EAD的度数;
(3)拓展延伸
如图3,在(2)的条件下,取线段DE的中点M,连接AM、BM,若BC=4,则当△ABM是直角三角形时,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() ,
,![]() 轴交于点
轴交于点![]() ,
,![]() ,与反比例函数的图象分别交于点
,与反比例函数的图象分别交于点![]() ,
,![]() ,
, ![]() 轴于点
轴于点![]() ,
, ![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)求反比例函数的解析式;
(3)连接![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售800只A型和450只B型的利润为210元,销售400只A型和600只B型的利润为180元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x只,这2000只口罩的销售总利润为y元.
①求y关于x的函数关系式;
②该药店购进A型、B型口罩各多少只,才能使销售总利润最大?
(3)在销售时,该药店开始时将B型口罩提价100%,当收回成本后,为了让利给消费者,决定把B型口罩的售价调整为进价的15%,求B型口罩降价的幅度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com