
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
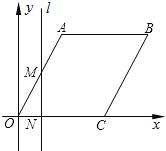
A. B.
B.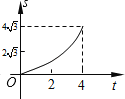
C. D.
D.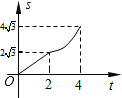
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点D、E分别在AB、AC上,要得到△ABE≌△ACD,可添加条件( )

A. ∠A=∠AB. ∠ABC=∠ACBC. BE=CDD. AD=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校初中各年级学生每天的平均睡眠时间(单位:![]() ,精确到
,精确到![]() ,抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
,抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_____,所抽查的学生人数为______.
的值为_____,所抽查的学生人数为______.
(2)求出平均睡眠时间为8小时的人数,并补全条形统计图.
(3)求出这部分学生的平均睡眠时间的众数和平均数.
(4)如果该校共有学生1800名,请你估计睡眠不足(少于8小时)的学生数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边平行于坐标轴,对角线BD经过坐标原点,点C在反比例函数y=![]() 的图象上.若点A的坐标为(﹣2,﹣2),则k=( )
的图象上.若点A的坐标为(﹣2,﹣2),则k=( )

A. 2 B. 4 C. 8 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假降至,丹尼斯大卖场为回馈新老顾客,进行有奖促销活动活动. 活动规定:购买500元的商品就可以获得一次转转盘的机会(转盘分为5个区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件(如果指针恰好停在分割线上,那么重转一次,直到指针指向某一区域为止). 大卖场工作人员在制作转盘时,将各扇形区域圆心角(不完全)分配如下表:
奖次 | 特等奖 | 一等奖 | 二等奖 | 三等奖 | 不获奖 |
圆心角 |
|
|
|
| _________ |
促销公告:凡购买我大卖场商品500元均有可能获得下列奖品:
特等奖:山地越野自行车一辆 一等奖:双肩背包一个
二等奖:洗衣液一桶 三等奖:抽纸一盒
根据以上信息,解答下列问题:
(1)求不获奖的扇形区域圆心角度数是多少?
(2)求获得双肩背包的概率是多少?
(3)甲顾客购物520元,求他获奖的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠A=40°.点P是射线AB上一动点(与点A不重合),CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F.
(1)求∠ECF的度数;
(2)随着点P的运动,∠APC与∠AFC之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由;
(3)当∠AEC=∠ACF时,求∠APC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com