
已知,如图,在Rt△ABC中,∠C=90º,∠BAC的角平分线AD交BC边于D。
(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹),再判断直线BC与⊙O的位置关系,并说明理由;
(2)若(1)中的⊙O与AB边的另一个交点为E,半径为2,AB=6, 求线段AD、AE与劣弧DE所![]() 围成的图形
围成的图形![]() 面积.(结果保留根号和
面积.(结果保留根号和![]() ) 《根据2011江苏扬州市中考试题改编》
) 《根据2011江苏扬州市中考试题改编》
解:(1)如图,作AD的垂直平分线交AB于点O,O为圆心,OA为半径作圆。
……………………………………………………………………………………(1分)
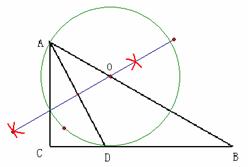
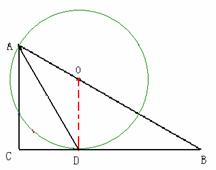
判断结果:BC是⊙O的切线。连结OD。 …………………………………………(1分)
∵AD平分∠BAC ∴∠DAC=∠DAB
∵OA=OD ∴∠ODA=∠DAB
∴∠DAC=∠ODA ∴OD∥AC ∴∠ODB=∠C
∵∠C=90º ∴∠ODB=90º 即:OD⊥BC
∵OD是⊙O的半径 ∴ BC是⊙O的切线。…………………………………(2分)
(2) 如图 ∵r=2 ∴OB=4 ∴∠OBD=30º,∠DOB=60º
∵△ODA的面积为![]()
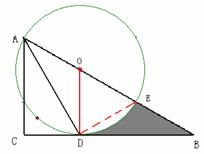 扇形ODE的面积为
扇形ODE的面积为![]() …………………………………………(1分)
…………………………………………(1分)
∴阴影部分的面积为![]() ……………(1分)
……………(1分)


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
 (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.| 3 |
| 5 |
| 14 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com