
【题目】点 O 是直线 AB上一点,∠COD 是直角,OE平分∠BOC.
(1)①如图1,若∠DOE=25°,求∠AOC 的度数;
②如图2,若∠DOE=α,直接写出∠AOC的度数(用含α的式子表示);
(2)将图 1中的∠COD 绕点O按顺时针方向旋转至图 2 所示位置.探究∠DOE 与∠AOC 的度数之间的关系,写出你的结论,并说明理由.

【答案】(1)①∠AOC=50°;②∠AOC=2α;(2)∠DOE=![]() ∠AOC,理由详见解析.
∠AOC,理由详见解析.
【解析】
(1)①首先求得∠COE的度数,然后根据角平分线的定义求得∠COB的度数,再根据∠AOC=180°﹣∠BOC即可求解;
②解法与①相同,把①中的25°改成α即可;
(2)把∠AOC的度数作为已知量,求得∠BOC的度数,然后根据角的平分线的定义求得∠COE的度数,再根据∠DOE=∠COD﹣∠COE求得∠DOE,即可解决.
(1)①∵∠COD=90°,∠DOE=25°,
∴∠COE=∠COD﹣∠DOE=90°﹣25°=65°,
又∵OE平分∠BOC,
∴∠BOC=2∠COE=130°,
∴∠AOC=180°﹣∠BOC=180°﹣130°=50°;
②∵∠COD=90°,∠DOE=α,
∴∠COE=∠COD﹣∠DOE=90°﹣α,
又∵OE平分∠BOC,
∴∠BOC=2∠COE=180°﹣2α,
∴∠AOC=180°﹣∠BOC=180°﹣(180°﹣2α)=2α;
(2)∠DOE=![]() ∠AOC,理由如下:
∠AOC,理由如下:
∵∠BOC=180°﹣∠AOC,
又∵OE平分∠BOC
∴∠COE=![]() ∠BOC=
∠BOC=![]() (180°﹣∠AOC)=90°﹣
(180°﹣∠AOC)=90°﹣![]() ∠AOC,
∠AOC,
又∵∠COD=90°,
∴∠DOE=90°﹣∠COE=90°﹣(90°﹣![]() ∠AOC)=
∠AOC)=![]() ∠AOC.
∠AOC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD. 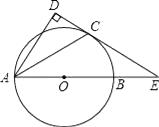
(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别是BC、CD上的点,且CE=CF,点P、Q分别是AF、EF的中点,连接PD、PQ、DQ,则△PQD的形状是( )
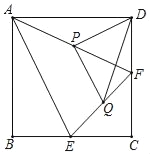
A. 等腰三角形 B. 直角三角形
C. 等腰非直角三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某广告公司招标了一批灯箱加工工程,需要在规定时间内加工1400个灯箱,该公司按一定速度加工5天后,发现按此速度加工下去会延期10天完工,于是又抽调了一批工人投入灯箱加工,使工作效率提高了50%,结果如期完成工作.
(1)求该公司前5天每天加多少个灯箱;
(2)求规定时间是多少天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: ①4a﹣b<0;
②abc<0;
③a+b+c<0;
④a﹣b+c>0;
⑤4a+2b+c>0.
其中错误的个数有( )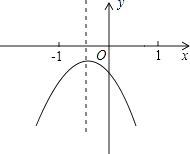
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com