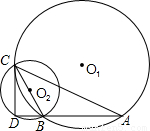
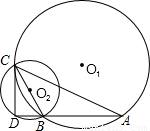
分析:(1)要证DC是⊙O1的切线,只要连接O1C,求证∠O1CD=90°即可;
(2)运用切割线定理DB的长,再运用勾股定理求出BC的长,再证明△BCD∽△CEB,解得CE=5.
解答: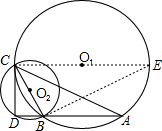
(1)证明:
证法一:过点C作⊙O
1的直径CE,并连接BE(1分)
∵∠BCD=∠A,∠E=∠A
∴∠BCD=∠E(3分)
∵CE为⊙O
1的直径
∴∠CBE=90°(4分)
∴∠E+∠ECB=90°
∴∠BCD+∠ECB=90°
即EC⊥CD
∴CD为⊙O
1的切(6分)
证法二:过C作⊙O
1的直径CE,连AE,利用圆内接四边形的外角的性质进行证明.
证法三:连OO
1、O
1O
2并延长O
1O
2交
于点M,利用圆心角关系进行证明.
(2)解:
解法一:∵CD为⊙O
1的切线
∴CD
2=DB•DA=DB•(DB+AB)由CD=2,AB=3
解得DB=1,DB=-4(舍去)(8分)
∵CB为⊙O
2的直径
∴∠D=90°,则
BC===(9分)
∴△BCD∽△CEB
∴
=∴
=,解得CE=5.(12分)
解法二:在求出DB=1的基础上,过O作OF⊥AB垂足为F,由四边形O
1CDF是矩形进行解答;
解法三:在求出DB=1的基础上,由△O
1O
2C∽△COB可求出半径;
解法四:在求出DB=1的基础上,根据勾股定理,求AC;由△CDB∽△CAE可求出直径.
点评:本题考查的是切线的判定,同时考查了相似三角形的判定和性质,切割线定理,勾股定理.

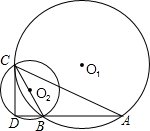 ∠A.
∠A. (1)证明:
(1)证明: