
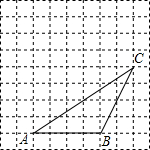
 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个单位长度.分析 (1)找到A、B、C三点的对应点再顺次连接即可;
(2)根据平移的性质可得这两条线段的关系是平行且相等;
(3)把五边形A′ABCC′放入一个矩形内,再利用矩形面积减去周围多与三角形的面积即可.
解答 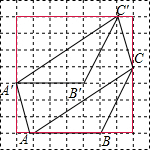 解:(1)如图所示:
解:(1)如图所示:
(2)这两条线段的关系是平行且相等;
(3)7×7-$\frac{1}{2}×4×6$-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4-$\frac{1}{2}×1×3$=49-12-1.5-4-1.5=30.
点评 此题主要考查了平移作图,以及计算图形的面积,关键是掌握作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
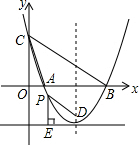 已知抛物线y=$\frac{1}{2}$x2+2(m+1)x-m+1与x轴交于点A、B,与y轴交于点C,其对称轴是直线x=4.
已知抛物线y=$\frac{1}{2}$x2+2(m+1)x-m+1与x轴交于点A、B,与y轴交于点C,其对称轴是直线x=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
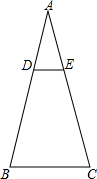 如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )
如图,在△ABC中,DE∥BC,且$\frac{AE}{EC}$=$\frac{1}{2}$,则$\frac{{S}_{四边形DBCE}}{{S}_{△ABC}}$=( )| A. | 1:4 | B. | 1:9 | C. | 3:4 | D. | 8:9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com