
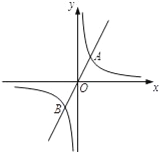
【题目】如图,正比例函数y=2x的图象与反比例函数y=![]() 的图象交于点A、B,AB=2
的图象交于点A、B,AB=2![]() ,
,
(1)求k的值;
(2)若反比例函数y=![]() 的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
的图象上存在一点C,则当△ABC为直角三角形,请直接写出点C的坐标.
【答案】(1)k=2(2)当△ABC为直角三角形,点C的坐标为(﹣4,﹣![]() )、(4,
)、(4,![]() )、(﹣2,﹣1)或(2,1)
)、(﹣2,﹣1)或(2,1)
【解析】分析:(1)过点A作AD⊥x轴,垂足为D,由点A、B的对称性可求出OA的值,根据点在直线上,设点A的坐标为(a,2a),在Rt△OAD中,通过勾股定理即可求出A的坐标,由点A的坐标利用待定系数法即可求出结论;
(2)由点A、B的对称性,结合点A的坐标求出点B的坐标,根据点C在反比例函数上,设出点C的坐标为(n,![]() ),分△ABC三个角分别为直角来考虑,利用“两直线垂直斜率之积为-1(斜率都存在)”求出点C的坐标.
),分△ABC三个角分别为直角来考虑,利用“两直线垂直斜率之积为-1(斜率都存在)”求出点C的坐标.
详解:(1)过点A作AD⊥x轴,垂足为D,如图1所示.
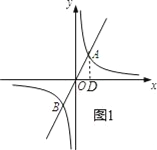
由题意可知点A与点B关于点O中心对称,且AB=2![]() ,∴OA=OB=
,∴OA=OB=![]() .
.
设点A的坐标为(a,2a),在Rt△OAD中,∠ADO=90°,由勾股定理得:
a2+(2a)2=(![]() )2,解得:a=1,∴点A的坐标为(1,2).
)2,解得:a=1,∴点A的坐标为(1,2).
把A(1,2)代入y=![]() 中得:2=
中得:2=![]() ,解得:k=2.
,解得:k=2.
(2)∵点A的坐标为(1,2),点A、B关于原点O中心对称,
∴点B的坐标为(﹣1,﹣2).设点C的坐标为(n,![]() ),
),
△ABC为直角三角形分三种情况:
①∠ABC=90°,则有AB⊥BC,![]() =﹣1,即n2+5n+4,
=﹣1,即n2+5n+4,
解得:n1=﹣4,n2=﹣1(舍去),此时点C的坐标为(﹣4,﹣![]() );
);
②∠BAC=90°,则有BA⊥AC,![]() =﹣1,即n2﹣5n+4=0,
=﹣1,即n2﹣5n+4=0,
解得:n3=4,n4=1(舍去),此时点C的坐标为(4,![]() );
);
③∠ACB=90°,则有AC⊥BC,![]() =﹣1,即n2=4,解得:n5=﹣2,n6=2,
=﹣1,即n2=4,解得:n5=﹣2,n6=2,
此时点C的坐标为(﹣2,﹣1)或(2,1).综上所述:当△ABC为直角三角形,点C的坐标为(﹣4,﹣![]() )、(4,
)、(4,![]() )、(﹣2,﹣1)或(2,1).
)、(﹣2,﹣1)或(2,1).


科目:初中数学 来源: 题型:
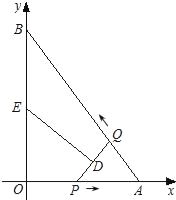
【题目】如图,在平面直角坐标系xOy中,直线AB与x轴交于点A,与y轴交于点B,且OA=3,AB=5.点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AO返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB﹣BO﹣OP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)求直线AB的解析式;
(2)在点P从O向A运动的过程中,求△APQ的面积S与t之间的函数关系式(不必写出t的取值范围);
(3)在点E从B向O运动的过程中,完成下面问题:
①四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,请说明理由;
②当DE经过点O时,请你直接写出t的值.
【答案】(1)直线AB的解析式为![]() ;(2)S=﹣
;(2)S=﹣![]() t2+
t2+![]() t;
t;
(3)四边形QBED能成为直角梯形.①t=![]() ;②当DE经过点O时,t=
;②当DE经过点O时,t=![]() 或
或![]() .
.
【解析】分析:(1)首先由在Rt△AOB中,OA=3,AB=5,求得OB的值,然后利用待定系数法即可求得一次函数的解析式;
(2)过点Q作QF⊥AO于点F.由△AQF∽△ABO,根据相似三角形的对应边成比例,借助于方程即可求得QF的长,然后即可求得![]() 的面积S与t之间的函数关系式;
的面积S与t之间的函数关系式;
(3)①分别从DE∥QB与PQ∥BO去分析,借助于相似三角形的性质,即可求得t的值;
②根据题意可知即![]() 时,则列方程即可求得t的值.
时,则列方程即可求得t的值.
详解:(1)在Rt△AOB中,OA=3,AB=5,由勾股定理得![]()
∴A(3,0),B(0,4).
设直线AB的解析式为y=kx+b.
∴![]() .解得
.解得
∴直线AB的解析式为![]()
(2)如图1,过点Q作QF⊥AO于点F.
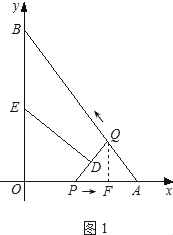
∵AQ=OP=t,∴AP=3t.
由△AQF∽△ABO,得![]()
∴![]()
∴![]()
∴![]()
∴![]()
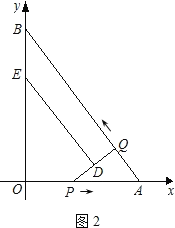
(3)四边形QBED能成为直角梯形,
①如图2,当DE∥QB时,
∵DE⊥PQ,
∴PQ⊥QB,四边形QBED是直角梯形.
此时![]()
由△APQ∽△ABO,得![]()
∴![]()
解得![]()
如图3,当PQ∥BO时,
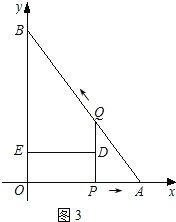
∵DE⊥PQ,
∴DE⊥BO,四边形QBED是直角梯形.
此时![]()
由△AQP∽△ABO,得![]()
即![]()
3t=5(3t),
3t=155t,
8t=15,
解得![]()
(当P从A向0运动的过程中还有两个,但不合题意舍去).
②当DE经过点O时,
∵DE垂直平分PQ,
∴EP=EQ=t,
由于P与Q相同的时间和速度,
∴AQ=EQ=EP=t,
∴∠AEQ=∠EAQ,
∵![]()
∴∠BEQ=∠EBQ,
∴BQ=EQ,
∴![]()
所以![]()
当P从A向O运动时,
过点Q作QF⊥OB于F,
EP=6t,
即EQ=EP=6t,
AQ=t,BQ=5t,
∴![]()
∴![]()
∵![]()
即![]()
解得:![]()
∴当DE经过点O时, ![]() 或
或![]() .
.
点睛:本题考查知识点较多,勾股定理,待定系数法求一次函数解析式,相似三角形的判定与性质等知识点,熟练掌握和运用各个知识点是解题的关键.
【题型】解答题
【结束】
21
【题目】如图,反比例函数y=(m≠0)与一次函数y=kx+b(k≠0)的图象相交于A、B两点,点A的坐标为(-6,2),点B的坐标为(3,n).求反比例函数和一次函数的解析式.
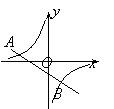
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的身体素质,某校坚持长年的全员体育锻炼,并定期进行体能测试,下面是将某班学生的立定跳远成绩(精确到0.01m),进行整理后,分成5组,画了的频率分布直方图的部分,已知:从左到右4个小组的频率分别是:0.05,0.15,0.30,0.35,第五小组的频数是9.
(1)该班参加测试的人数是多少?
(2)补全频率分布直方图.
(3)若该成绩在2.00m(含2.00)的为合格,问该班成绩合格率是多少?
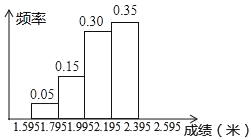
查看答案和解析>>
科目:初中数学 来源: 题型:
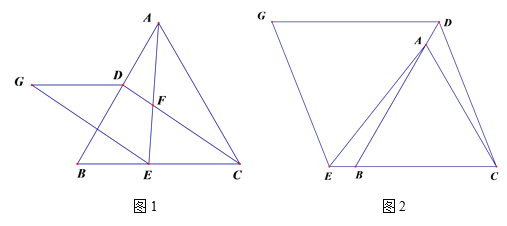
【题目】已知![]() ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
(1)如图1,若点D、E分别是AB、CB边上的点,连接AE、CD交于点F,过点E作∠AEG=60°,使EG=AE,连接GD,则∠AFD= (填度数);
(2)在(1)的条件下,猜想DG与CE存在什么关系,并证明;
(3)如图2,若点D、E分别是BA、CB延长线上的点,(2)中结论是否仍然成立?请给出判断并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为 BC上的点,F为 CD边上的点,且AE=AF,AB=4,设EC=x,△AEF 的面积为y,则y与x之间的函数关系式是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师打算在小明和小白两位同学之间选一位同学参加数学竞赛,他收集了小明、小白近期10次数学考试成绩,并绘制了折线统计图(如图所示)
项目 | 众数 | 中位数 | 平均数 | 方差 | 最高分 |
小明 | 85 | 85 | |||
小白 | 70,100 | 85 | 100 |
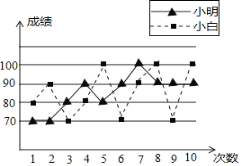
(1)根据折线统计图,张老师绘制了不完整的统计表,请你补充完整统计表;
(2)你认为张老师会选择哪位同学参加比赛?并说明你的理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “清明时节雨纷纷”是必然事件
B. 了解路边行人边步行边低头看手机的情况可以采取对在路边行走的学生随机发放问卷的方式进行调查
C. 射击运动员甲、乙分别射击10次且击中环数的方差分别是0.5和1.2,则甲队员的成绩好
D. 分别写有三个数字 -1,-2,4的三张卡片(卡片的大小形状都相同),从中任意抽取两张,则卡片上的两数之积为正数的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
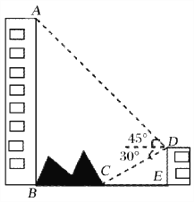
【题目】如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上). 已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果精确到0.1m)
(参考数据: ![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各小题中,都有OE平分∠AOC,OF平分∠BOC.
(1)如图,若点A.O.B在一条直线上,则∠AOB与∠EOF的数量关系是:∠AOB=_____∠EOF.
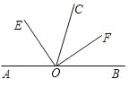
(2)如图,若点A.O.B不在一条直线上,则题(1)中的数量关系是否成立?请说明理由.
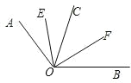
(3)如图,若OA在∠BOC的内部,则题(1)中的数量关系是否仍成立?请说明理由
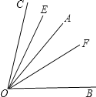
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com