
【题目】某工厂准备在春节前生产甲、乙两种型号的新年礼盒共 80 万套,两种礼盒的成本和售价如下表所示;
甲 | 乙 | |
成本(元/套) | 25 | 28 |
售价(元/套) | 30 | 38 |
(1)该工厂计划筹资金 2150 万元,且全部用于生产甲乙两种礼盒,则这两种礼盒各生产多少万套?
(2)经过市场调查,该厂决定在原计划的基础上增加生产甲种礼盒![]() 万套,增加生产乙种礼盒
万套,增加生产乙种礼盒![]() 万套(
万套(![]() ,
,![]() 都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
都为正整数),且两种礼盒售完后所获得的总利润恰为 690 万元,请问该工厂有几种生产方案?并写出所有可行的生产方案.
(3)在(2)的情况下,设实际生产的两种礼盒的总成本为![]() 万元,请写出
万元,请写出![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当 ![]() 为多少时成本
为多少时成本![]() 有最小值,并求出成本
有最小值,并求出成本![]() 的最小值为多少万元?
的最小值为多少万元?
【答案】(1)甲礼盒生产30万套,乙礼盒生产50万套;(2)方案如下:①![]() ;②
;②![]() ;③
;③![]() ;(3)
;(3)![]() 时,
时,![]() 最小值为
最小值为![]() 万元.
万元.
【解析】
(1)设甲礼盒生产![]() 万套,乙礼盒生产
万套,乙礼盒生产![]() 万套,从而列出相应的方程,即可解答本题;
万套,从而列出相应的方程,即可解答本题;
(2)根据表格可以求得A的利润与B的利润,从而可以求得总利润,写出相应的关系式,再利用正整数的特性得出可行的生产方案;
(3)根据表格的数据,列出相应的函数关系式,利用一次函数的增减性即可成本![]() 的最小值.
的最小值.
(1)设甲礼盒生产![]() 万套,乙礼盒生产
万套,乙礼盒生产![]() 万套,
万套,
依题意得:![]() ,
,
解得:![]() ,
,
答:甲礼盒生产30万套,乙礼盒生产50万套;
(2)增加生产后,甲![]() 万套,乙
万套,乙![]() 万套,
万套,
依题意得:![]() ,
,
化简得:![]() ,
,
∴方案如下:
![]() ;
;
![]() ;
;
![]() ;
;
答:有三种方案,![]() ,
,![]() ,
,![]() ;
;
(3)依题意得:![]() ,
,
化简得:![]() ,
,
∵![]() ,
,
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
∴![]() 取最小值时
取最小值时![]() 最小,
最小,
∴![]() 时,
时, ![]() (万元).
(万元).
答:当![]() 时,
时,![]() 最小值为
最小值为![]() 万元.
万元.


科目:初中数学 来源: 题型:
【题目】某甜品店用![]() ,
,![]() 两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品
两种原料制作成甲、乙两款甜品进行销售,制作每份甜品的原料所需用量如下表所示.该店制作甲款甜品![]() 份,乙款甜品
份,乙款甜品![]() 份,共用去
份,共用去![]() 原料2000克.
原料2000克.
原料 款式 |
(克) |
(克) |
甲款甜品 | 30 | 15 |
乙款甜品 | 10 | 20 |
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)已知每份甲甜品的利润为5元,每份乙甜品的利润为2元.假设两款甜品均能全部卖出.若获得总利润不少于360元,则至少要用去![]() 原料多少克?
原料多少克?
查看答案和解析>>
科目:初中数学 来源: 题型:
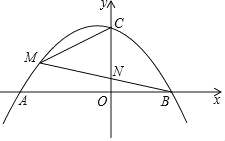
【题目】如图,抛物线y=ax2+ax﹣12a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,点M是第二象限内抛物线上一点,BM交y轴于N.
(1)求点A、B的坐标;
(2)若BN=MN,且S△MBC=![]() ,求a的值;
,求a的值;
(3)若∠BMC=2∠ABM,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学决定在“五·四艺术周”为一个节目制作A、B两种道具,共80个. 制作的道具需要甲、乙两种材料组合而成,现有甲种材料700件,乙种材料500件,已知组装A、B两种道具所需的甲、乙两种材料,如下表所示:
甲种材料(件) | 乙种材料(件) | |
A道具 | 6 | 8 |
B道具 | 10 | 4 |
经过计算,制作一个A道具的费用为5元,一个B道具的费用为4.5元. 设组装A种道具x个,所需总费用为y元.
(1)求y与x的函数关系式,并求出x的取值范围;
(2)问组装A种道具多少个时,所需总费用最少,最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明随机抽取了某校八年级部分学生,针对他们晚上在家学习时间的情况进行调查,并将调查结果绘制成如下两幅尚不完整的统计图.根据以上信息,解答下列问题:
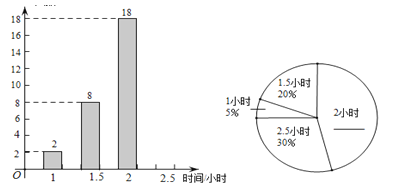
(1)补全条形统计图和扇形统计图;
(2)本次抽取的八年级学生晚上学习时间的众数是 小时,中位数是 小时;
(3)若该校共有 600 名八年级学生,则晚上学习时间超过 1.5 小时的约有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
如图1,在![]() 中,
中,![]() 平分
平分![]() ,
,![]() .求证:
.求证:![]()
小明通过思考发现,可以通过“截长、补短”两种方法解决问题:
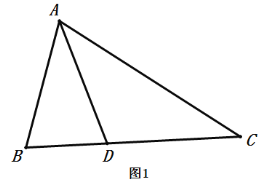
方法1:如图2,在![]() 上截取
上截取![]() ,使得
,使得![]() ,连接
,连接![]() ,可以得到全等三角形,进而解决问题
,可以得到全等三角形,进而解决问题
方法二:如图3,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,可以得到等腰三角形,进而解决问题
,可以得到等腰三角形,进而解决问题
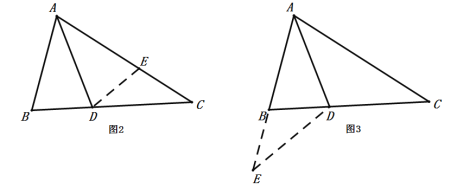
(1)根据阅读材料,任选一种方法证明![]()
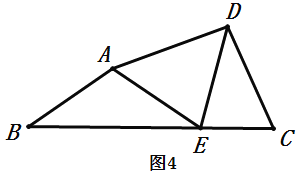
(2)根据自己的解题经验或参考小明的方法,解决下面的问题:如图4,四边形![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() ,探究
,探究![]() 、
、![]() 、
、![]() 之间的数量关系,并证明
之间的数量关系,并证明
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解黔东南州某县2013届中考学生的体育考试得分情况,从该县参加体育考试的4000名学生中随机抽取了100名学生的体育考试成绩作样本分析,得出如下不完整的频数统计表和频数分布直方图.
成绩分组 | 组中值 | 频数 |
25≤x<30 | 27.5 | 4 |
30≤x<35 | 32.5 | m |
35≤x<40 | 37.5 | 24 |
40≤x<45 | a | 36 |
45≤x<50 | 47.5 | n |
50≤x<55 | 52.5 | 4 |
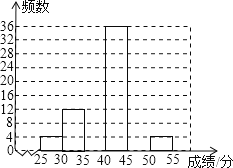
(1)求a、m、n的值,并补全频数分布直方图;
(2)若体育得分在40分以上(包括40分)为优秀,请问该县中考体育成绩优秀学生人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
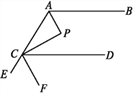
【题目】如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
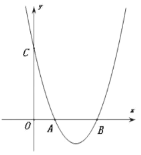
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(3)在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com