
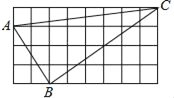
【题目】如图,正方形网格中有△ABC,若小方格边长为1,请你根据所学的知识解答下列问题:
(1)判断△ABC是什么形状?并说明理由.
(2)求△ABC中BC边上的高.
科目:初中数学 来源: 题型:
【题目】某校招聘一名数学老师,对应聘者分别进行了教学能力、科研能力和组织能力三项测试,其中甲、乙两名应聘者的成绩如右表:(单位:分)
教学能力 | 科研能力 | 组织能力 | |
甲 | 81 | 85 | 86 |
乙 | 92 | 80 | 74 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将被录用?
(2)根据实际需要,学校将教学、科研和组织能力三项测试得分按 5:3:2 的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.

查看答案和解析>>
科目:初中数学 来源: 题型:
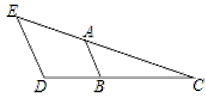
【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么 ![]() 的值是 .
的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距 千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
(5)若B的自行车不发生故障,保持出发时的速度前进, 小时与A相遇,相遇点离B的出发点 千米.在图中表示出这个相遇点C.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A. 
(1)求证:AC=AF;
(2)在边AB的下方画∠GBA=∠CED,交CF的延长线于点G,联结DG,在图中画出图形,并证明四边形CDGB是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
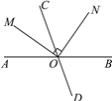
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.
(1)若∠BOD=70°,求∠AOM和∠CON的度数;
(2)若∠BON=50°,求∠AOM和∠CON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边长为8cm,腰长为5cm,一动点P在底边上从B向C以0.25cm/s的速度移动,请你探究:当P运动几秒时,P点与顶点A的连线PA与腰垂直。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com