
【题目】目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.

(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米).
(参考数据:sin39°≈0.6293,cos39°≈0.7771,tan39°≈0.8100)
【答案】(1)大楼与电视塔之间的距离AC为610米;(2)大楼的高度CD约为116米.
【解析】试题(1)由于∠ACB=45°,∠A=90°,因此△ABC是等腰直角三角形,所以AC=AB=610米;
(2)根据矩形的对边相等可知:DE=AC=610米.在Rt△BDE中,运用直角三角形的边角关系即可求出BE的长,CD=AB-BE.
试题解析:(1)在Rt△BAC中,∠ACB=45°,∠A=90°,
∴△BAC是等腰直角三角形.
∴AC=AB=610米.
∴大楼与电视塔之间的距离AC为610米.
(2)作DE∥AC交AB于点E,
则∠BDE=39°,DE=AC=610米.
在Rt△BED中,BE=DEtan39°≈494.0米.
则CD=AE=AB-BE=610-494.0116≈116米.
则大楼的高度CD约为116米.
考点: 解直角三角形的应用-仰角俯角问题.


科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 外一点,
外一点,![]() ,
,![]() ,
,![]()

(1)求四边形![]() 的面积
的面积
(2)若![]() 为
为![]() 内一点,其它条件不变,请画出图形并判断四边形
内一点,其它条件不变,请画出图形并判断四边形![]() 的面积是否有变化.若有变化请求出四边形
的面积是否有变化.若有变化请求出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
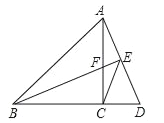
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC的延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE.
(1)求证:△BCF≌△ACD.
(2)猜想∠BEC的度数,并说明理由;
(3)探究线段AE,BE,CE之间满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x(元) | 3000 | 3200 | 3500 | 4000 |
y(辆) | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求按照表格呈现的规律,每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数(辆) | ________ | 未租出的车辆数(辆) | ________ |
租出每辆车的月收益(元) | ________ | 所有未租出的车辆每月的维护费(元) | ________ |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩x(分) | 频数(人数) | 频率 |
一 | 50≤x<60 | 2 | 0.04 |
二 | 60≤x<70 | 10 | 0.2 |
三 | 70≤x<80 | 14 | b |
四 | 80≤x<90 | a | 0.32 |
五 | 90≤x<100 | 8 | 0.16 |
请根据表格提供的信息,解答以下问题:

(1)直接写出表中a=________,b=________;
(2)请补全右面相应的频数分布直方图;
(3)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为________.
(4)请根据得到的统计数据,简要分析这些同学的汉字书写能力,并为提高同学们的书写汉字能力提一条建议(所提建议不超过20字).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
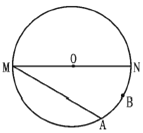
【题目】如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为![]() 的中点,P是直径MN上一动点.
的中点,P是直径MN上一动点.
(1)利用尺规作图,确定当PA+PB最小时P点的位置(不写作法,但要保留作图痕迹).
(2)求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。

(1)如图1,直接写出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)当x为何值时,y>0?当x为何值时,y<0?
(3)写出y随x的增大而减小的自变量x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com