
 如图,∠ABC=90°,∠CBD=30°,BP平分∠ABC,求∠DBP的度数.
如图,∠ABC=90°,∠CBD=30°,BP平分∠ABC,求∠DBP的度数.  53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
| A. | x=0 | B. | x1=0,x2=4 | ||
| C. | x1=0,x2=$\frac{1}{4}$ | D. | x1=$\frac{1+\sqrt{17}}{8}$,x2=$\frac{1-\sqrt{17}}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>0 | B. | k<0 | C. | k$>-\frac{1}{8}$ | D. | k$<-\frac{1}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2x2-1=3x | B. | 2x2-y=1 | C. | ax2+bx+c=0 | D. | 2x2+$\frac{1}{x}$=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
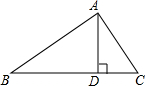 如图所示,在△ABC中,作BC边上的高AD,则△ABC的面积S=$\frac{1}{2}$BC•AD,而在Rt△ABD中,sinB=$\frac{AD}{AB}$,所以AD=AB•sinB.因此,△ABC的面积S=$\frac{1}{2}AB•BC•sinB$.
如图所示,在△ABC中,作BC边上的高AD,则△ABC的面积S=$\frac{1}{2}$BC•AD,而在Rt△ABD中,sinB=$\frac{AD}{AB}$,所以AD=AB•sinB.因此,△ABC的面积S=$\frac{1}{2}AB•BC•sinB$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
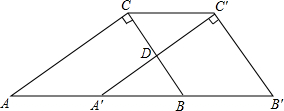 已知:如图,在Rt△ABC中.∠ACB=Rt∠,AC=4,BC=3.将△ABC沿AB方向平移至△A′B′C,使A′C′经过BC的中点D.
已知:如图,在Rt△ABC中.∠ACB=Rt∠,AC=4,BC=3.将△ABC沿AB方向平移至△A′B′C,使A′C′经过BC的中点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,P是△ABC的边AB上一点,请添加一个条件使得△ABC与△ACP相似,则你添加的条件可以是∠B=∠ACP.(只需添加一个符合的条件即可)
如图,P是△ABC的边AB上一点,请添加一个条件使得△ABC与△ACP相似,则你添加的条件可以是∠B=∠ACP.(只需添加一个符合的条件即可)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com