
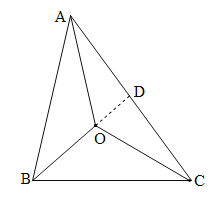
【题目】已知点O在![]() 内部,连接OA,OB,OC,说明:
内部,连接OA,OB,OC,说明:![]() .
.
【答案】证明见解析
【解析】
延长BO交AC于D.在△AOB、△BOC、△AOC中,由三角形三边关系定理列式,三式相加可得2(OA+OB+OC)>AB+BC+AC,即可证明不等式左边部分成立.在△ADO、△BDC中,由三角形三边关系定理列式,两式相加可得OA+BO<AC+BC,同理可得:OC+OB<AB+AC,OC+OA<AB+BC,三式相加即可证明不等式右边部分成立.
延长BO交AC于D.
在![]() 中,
中,![]() ,①
,①
在![]() 中
中![]() ,②
,②
在![]() 中,
中,![]() ,③
,③
①+②+③得![]() .
.
即![]() .
.
在△ADO中,OA<AD+OD,
在△BDC中,BD<DC+BC,
∴OA+BD<AD+OD+DC+BC,
即OA+BO+OD<AC+OD+BC,
∴OA+BO<AC+BC ④
同理:![]() ⑤
⑤
![]() ,⑥
,⑥
④+⑤+⑥得![]() ,
,
即![]() .
.
∴![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2017OB2017.则点B2017的坐标_______

查看答案和解析>>
科目:初中数学 来源: 题型:
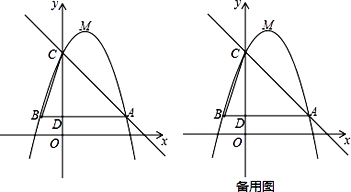
【题目】如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥ x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ ABC的内部(不包括△ ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△ BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
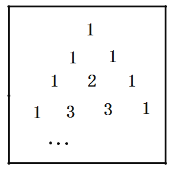
【题目】我国宋朝数学家杨在他的著作《详解九章算法》中提出“杨辉三角”(如图所示),此图揭示了![]() (n为非负整数)展开式的项数及各项系数的有关规律.
(n为非负整数)展开式的项数及各项系数的有关规律.
例如:![]() ,它只有一项,系数为1;
,它只有一项,系数为1;![]() ,它有两项,系数分别为1,1,系数和为2;
,它有两项,系数分别为1,1,系数和为2;![]() ,它有三项,系数分别为1,2,1,系数和为4;
,它有三项,系数分别为1,2,1,系数和为4;![]() ,它有四项系数分别为1,3,3,1,系数和为8;……根据以上规律,解答下列问题:
,它有四项系数分别为1,3,3,1,系数和为8;……根据以上规律,解答下列问题:
(1)![]() 展开式共有________项,系数分别为________.
展开式共有________项,系数分别为________.
(2)![]() 展开式共有________项,系数和为________.
展开式共有________项,系数和为________.
(3)![]() 展开结果为________.
展开结果为________.
(4)利用上面的规律计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
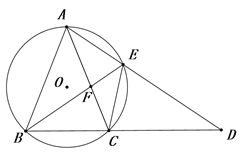
【题目】如图,△ABC内接于⊙O,且AB=AC.延长BC到点D,使CD=CA,连接AD交⊙O于点E.
(1)求证:△ABE≌△CDE;
(2)填空:
①当∠ABC的度数为 时,四边形AOCE是菱形;
②若AE=6,BE=8,则EF的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售功能相同的两种品牌的计算器,购买2个A品牌和1个B品牌的计算器共需122元;购买1个A品牌和2个B品牌的计算器共需124元.
(1)求这两种品牌计算器的单价;
(2)学校开学前夕,该商店举行促销活动,具体办法如下:购买A品牌计算器按原价的九折销售,购买B品牌计算器超出10个以上超出的部分按原价的八折销售,①设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1、y2关于x的函数关系式;
②小明准备联系一部分同学集体购买同一品牌的计算器,若购买计算器的数量超过10个,问购买哪种品牌的计算器更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD中,点E为BC边上任意一点(点E不与B,C重合),点F在线段AE上,过点F的直线![]() ,分别交AB、CD于点M、N.
,分别交AB、CD于点M、N.
(1)如图,求证:![]() ;
;
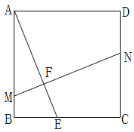
(2)如图,当点F为AE中点时,连接正方形的对角线BD,MN与BD交于点G,连接BF,求证:![]() ;
;
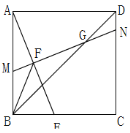
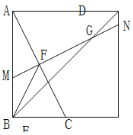
(3)如图,在(2)的条件下,若![]() ,
,![]() ,求BM的长度.
,求BM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在直线AB上,OC、OD是两条射线,OC⊥OD,射线OE平分∠BOC.
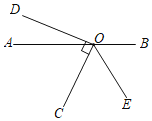
(1)若∠DOE=150°,求∠AOC的度数.
(2)若∠DOE=α,则∠AOC= .(请用含α的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com