

���� ��1����ֱ��AB�Ľ���ʽ�ɵó�OA=OB���Ӷ��ó���BAO=45�㣬��OFE=45�㣬��AFE=135�㣬����۵������ʿɵó���DFE=135�㣬�����ó���AFD=90�㣬��DF��x�ᣬDF��EH����������Ա߷ֱ�ƽ�м���֤���ı���DHEFΪƽ���ı��Σ�
��2���������ε����ʿɵó�EF=DF���Ӷ��ɵó�����ʱ��t��һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
��3�������ı���DCEF���ڵ�һ�����ڵ�ͼ�ε���״��ͬ������������ǣ������۵��������Լ������ε������ʽ���ɵó����ۣ�
��� ��1���������⻭��ͼ�Σ���ͼ1��ʾ��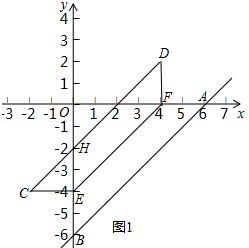
��ֱ��y=x-6��x�ᡢy��ֱ��ڵ�A��B��
��A��6��0����B��0��-6����
��OA=OB��
�ߡ�AOB=90�㣬
���BAO=45�㣬
��AB��EF��
���OFE=45�㣬��AFE=135�㣮
���۵������ʿ�֪����DFE=135�㣬
���AFD=90�㣬��DF��x�ᣬ
��DF��EH��
��DH��EF��
���ı���DHEFΪƽ���ı��Σ�
��2��Ҫʹƽ���ı���DHEFΪ���Σ�ֻ��EF=DF��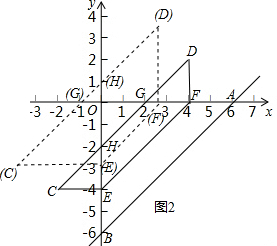
��$\sqrt{2}��6-t��=t$��
��$t=\frac{{6\sqrt{2}}}{{\sqrt{2}+1}}=12-6\sqrt{2}$��
��3��������������ۣ���ͼ2��ʾ����
�ٵ�0��t��3ʱ��
�ı���DCEF���ڵ�һ�����ڵ�ͼ���ǡ�DFG��
��ʱGF=DF=t��
��S=$\frac{1}{2}{t^2}$��
�ڵ�3��t��6ʱ��
�ı���DCEF���ڵ�һ�����ڵ�ͼ�������Σ�
��ʱDF=GF=t��OG=OH=2t-6��
��S=$\frac{1}{2}{t^2}$-$\frac{1}{2}$��2t-6��2=-$\frac{3}{2}{t}^{2}$+12t-18=$-\frac{3}{2}{��t-4��^2}+6$��
���Ͽ�֪��S��t�ĺ�������ʽΪS=$\left\{\begin{array}{l}{\frac{1}{2}{t}^{2}��0��t��3��}\\{-\frac{3}{2}��t-4��^{2}+6��3��t��6��}\end{array}\right.$��
���� ���⿼����ƽ���ı��ε��ж����۵������ʡ����ε������Լ������ε����������Ĺؼ��ǣ���1���ҳ�DF��EH����2���ҳ�����t��һԪһ�η��̣���3��������������ǣ����������е��⣬�ѶȲ������������Ŀʱ�������۵��������ҳ���ȵı߽ǹ�ϵ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ھ���ABCD�У���E��AD���е㣬BE��ֱAC��AC�ڵ�F����֤����DEF�ס�BED��
�ھ���ABCD�У���E��AD���е㣬BE��ֱAC��AC�ڵ�F����֤����DEF�ס�BED���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ������ABCD �У���AD ���е� E��AC �Ĵ���EF����AB �ڵ� M����CB ���ӳ����ڵ�F�����FB�ij��� $\sqrt{2}$����AEM=30�㣮������ABCD ���ܳ��������
��֪����ͼ������ABCD �У���AD ���е� E��AC �Ĵ���EF����AB �ڵ� M����CB ���ӳ����ڵ�F�����FB�ij��� $\sqrt{2}$����AEM=30�㣮������ABCD ���ܳ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��3 | B�� | x��2 | C�� | x��2 | D�� | 2��x��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y+3��x | B�� | 3-4��0 | C�� | 2x2-4��1 | D�� | 2-x��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 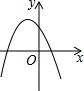 | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�AB=AC��AD�ǽ�ƽ���ߣ���E��AD�ϣ���д��ͼ������ȫ�������Σ���ѡ�����е�һ�Լ���֤����
��ͼ���ڡ�ABC�У�AB=AC��AD�ǽ�ƽ���ߣ���E��AD�ϣ���д��ͼ������ȫ�������Σ���ѡ�����е�һ�Լ���֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
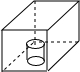 ��ͼ�������ˮ�۵ײ����ձ�עˮ������һ������ע���ձ�����עˮ��ֱ��ע��ˮ�ۣ�ˮ����ˮ�������߶�h��עˮʱ��Ĺ�ϵ����������ͼ���еģ�������
��ͼ�������ˮ�۵ײ����ձ�עˮ������һ������ע���ձ�����עˮ��ֱ��ע��ˮ�ۣ�ˮ����ˮ�������߶�h��עˮʱ��Ĺ�ϵ����������ͼ���еģ�������| A�� | 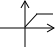 | B�� | 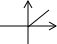 | C�� | 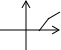 | D�� | 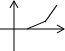 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com