
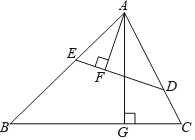
【题目】如图在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)如AF=3,AG=5,求△ADE与△ABC的周长之比.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形OBDC的对角线相交于点E,其中O(0,0),B(3,4),C(m,0),反比例函数y=![]() (k≠0)的图象经过点B.
(k≠0)的图象经过点B.
(1)求反比例函数的解析式;
(2)若点E恰好落在反比例函数y=![]() 上,求平行四边形OBDC的面积.
上,求平行四边形OBDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
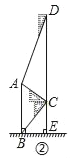
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73).
=1.73).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化工材料经销公司购进一种化工材料若干千克,价格为每千克40元,物价部门规定其销售单价不高于每千克70元,不低于每千克40元.经市场调查发现,日销量y(千克)是销售单价x(元)的一次函数,且当x=70时,y=80;x=60时,y=100.在销售过程中,每天还要支付其他费用350元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式;
(3)当销售单价为多少元时,该公司日获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3与x轴交于A.B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
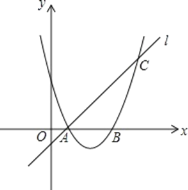
(1)求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组对角互补的四边形叫做互补四边形,如图,在互补四边形纸片ABCD中,BA=BC,AD=CD,∠A=∠C=90°,∠ADC=30°.将纸片先沿直线BD对折,再将对折后的纸片从一个顶点出发的直线裁剪,把剪开的纸片打开后铺平,若铺平后的纸片中有一个面积为4的平行四边形,则CD的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
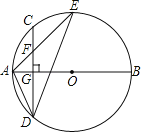
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;④S△DEF=4
;④S△DEF=4![]() .
.
其中正确的是 (写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
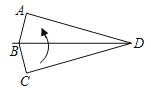
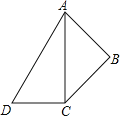
【题目】如图所示,将一副三角板摆放在一起,组成四边形ABCD,∠ABC=∠ACD=90°,∠ADC=60°,∠ACB=45°,连接BD,则tan∠CBD的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣1)2+4的图象经过点(﹣1,0).
(1)求这个二次函数的解析式;
(2)判断这个二次函数的开口方向,对称轴和顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com