
 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.| x | … | -3 | $-\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | 0 | $\frac{5}{4}$ | 3 | … |
分析 (1)将x=-2代入函数解析式中求出y值,即可得出结论;
(2)根据表格数据,描点补充完图形;
(3)根据函数图象,寻找出对称轴以及函数的单调区间,此题得解;
(4)①观察函数图象,根据函数图象与x轴有3个交点,即可得出结论;②画出直线y=2,观察图形,可得出函数y=x2-2|x|的图象与y=2只有2个交点,此题得解.
解答 解:(1)当x=-2时,y=(-2)2-2×|-2|=0,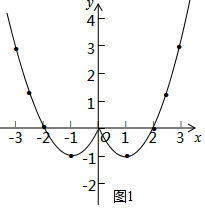
∴m=0,
故答案为:0.
(2)根据给定的表格中数据描点画出图形,如图1所示.
(3)观察函数图象,可得出:①函数图象关于y轴对称,②当x>1时,y随x的增大而增大.
(4)①观察函数图象可知:当x=-2、0、2时,y=0,
∴该函数图象与x轴有3个交点,
即对应的方程x2-2|x|=0有3个实数根.
故答案为:3;3.
②在图中作直线y=2,如图2所示.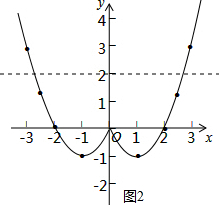
观察函数图象可知:函数y=x2-2|x|的图象与y=2只有2个交点.
故答案为:2.
点评 本题考查了抛物线与x轴的交点以及二次函数的性质,根据题意画出图形,利用数形结合解决问题是解题的关键.


科目:初中数学 来源: 题型:选择题
| 听 | 说 | 读 | 写 | |
| 张明 | 90 | 80 | 83 | 82 |
| A. | 82 | B. | 83 | C. | 84 | D. | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上的A、B、C三点所表示的数分别为a,b,c,其中AB的长度与BC的长度相等,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
如图,数轴上的A、B、C三点所表示的数分别为a,b,c,其中AB的长度与BC的长度相等,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )| A. | 点A的左边 | B. | 点A与点B之间,靠近点A | ||
| C. | 点B与点C之间,靠近点B | D. | 点C的右边 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.362×107 | B. | 83.62×106 | C. | 0.8362×108 | D. | 8.362×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com