【题目】某一广告墙PQ旁有两根直立的木杆AB和CD ， 某一时刻在太阳光下，木杆CD的影子刚好不落在广告墙PQ上，
（1）你在图中画出此时的太阳光线CE及木杆AB的影子BF；
（2）若AB=6米，CD=3米 ， CD到PQ的距离DQ的长为4米，求此时木杆AB的影长．
【答案】
（1）
解答：如图所示：
；
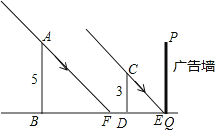（2）
设木杆AB的影长BF为x米，
由题意，得
，
解得 
．
答：木杆AB的影长是 
米．
【解析】根据木杆CD的影子刚好不落在广告墙上可以画出此时的太阳光线CE，根据太阳光线是平行的，可以画出木杆AB的影子BF；根据在同一时刻，物高与影子成比例进行求解．
【考点精析】通过灵活运用相似三角形的应用和平行投影，掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解；太阳光线可以看成是平行光线，平行光线所形成的投影称为平行投影；作物体的平行投影：由于平行投影的光线是平行的，而物体的顶端与影子的顶端确定的直线就是光线，故根据另一物体的顶端可作出其影子即可以解答此题．
考前必练系列答案科目：初中数学 来源： 题型：
【题目】七巧板是我们祖先的一项卓越创造，被誉为“东方魔板”，小明利用七巧板（如图1所示）中各板块的边长之间的关系拼成一个凸六边形（如图2所示），则该凸六边形的周长是cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若反比例函数 
的图象经过点（m ， 3m），其中m≠0，则此反比例函数图象经过（ ）
A.第一、三象限
B.第一、二象限
C.第二、四象限
D.第三、四象限
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠BAC=90°，BE平分∠ABC，AM⊥BC于点M，交BE于点G，AD平分∠MAC，交BC于点D，交BE于点F．
（1）判断直线BE与线段AD之间的关系，并说明理由；
（2）若∠C=30°，图中是否存在等边三角形？若存在，请写出来并证明；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一个几何体的形状为直三棱柱，右图是它的主视图和左视图．
（1）请补画出它的俯视图，并标出相关数据；
（2）根据图中所标的尺寸（单位：厘米），计算这个几何体的全面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线l上有一点O，点A，B同时从O出发，在直线l上分别向左，向右作匀速运动，且A，B的速度之比是1：2，设运动时间为ts，
（1）当t=2s时，AB=24cm，此时，
①在直线l上画出A，B两点运动2s时的位置，并回答点A运动的速度是 cm/s，点B的运动速度是 cm/s；
②若点P为直线l上一点，且PA=OP+PB，求
的值；
（2）在（1）的条件下，若A，B同时按原速度向左运动，再经过几秒，OA=3OB？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于O点，且BE=BF，∠BEF=2∠BAC。
（1）求证：OE=OF；
（2）若BC=
，求AB的长。
查看答案和解析>>
科目：初中数学 来源： 题型：
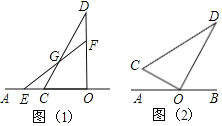
【题目】如图，已知点O在直线AB上，将一副直角三角板的直角顶点放在点O处，其中∠OCD=60°，∠OEF=45°．边OC、OE在直线AB上．
（1）如图（1），若CD和EF相交于点G，则∠DGF的度数是______°；
（2）将图（1）中的三角板OCD绕点O顺时针旋转30°至图（2）位置
①若将三角板OEF绕点O顺时针旋转180°，在此过程中，当∠COE=∠EOD=∠DOF时，求∠AOE的度数；
②若将三角板OEF绕点O以每秒4°的速度顺时针旋转180°，与此同时，将三角板OCD绕点O以每秒1°的速度顺时针旋转，当三角板OEF旋转到终点位置时，三角板OCD也停止旋转．设旋转时间为t秒，当OD⊥EF时，求t的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
