
【题目】一个有进水管与出水管的容器,从某时刻开始4 min内只进水不出水,在随后的8 min内既进水又出水,每分的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.

(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
【题目】为迎接“五一劳动节”,某超市开展促销活动,决定对A,B两种商品进行打折出售.打折前,买6件A商品和3件B商品需要108元,买3件A商品和4件B商品需要94元.问:打折后,若买5件A商品和4件B商品仅需86元,比打折前节省了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a>0)的两个实数根x1 , x2满足x1+x2=4和x1x2=3,那么二次函数ax2+bx+c(a>0)的图象有可能是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明题
(1)已知一元二次方程x2+px+q=0(p2-4q≥0)的两根为x1、x2;求证:x1+x2=-p , x1 x2=q .
(2)已知抛物线y=x2+px+q与x轴交于A、B两点,且过点(-1,-1),设线段AB的长为d,当p为何值时,d2取得最小值,并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在正是草莓热销的季节,某水果零售商店分两批次从批发市场共购进草莓40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进草莓的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱草莓先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部草莓所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.(注:按整箱出售,利润=销售总收入-进货总成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a,b满足![]() ,解关于x的方程(a+2)x+b2=a-1.
,解关于x的方程(a+2)x+b2=a-1.
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为![]() ,求代数式x2+(a+b)cdx+
,求代数式x2+(a+b)cdx+![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(﹣1,0)
注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(﹣ ![]() ,
, ![]() )
)
(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于不等式组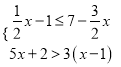 下列说法正确的是( )
下列说法正确的是( )
A. 此不等式组无解 B. 此不等式组有7个整数解
C. 此不等式组的负整数解是﹣3,﹣2,﹣1 D. 此不等式组的解集是![]() <x≤2
<x≤2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com