
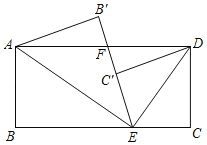
【题目】如图所示,在矩形ABCD中,AB=1,在线段BC上取一点E,连接AE、ED,将△ABE沿AE翻折,使点B落在B'处,线段EB'交AD于点F.将△ECD沿DE翻折,使点C的对应点C'落在线段EB'上,且点C'恰好为EB'的中点,则线段EF的长为_____.
【答案】![]()
【解析】
由折叠的性质可得AB=AB'=CD=C'D=1,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,由中点性质可得B'E=2C'E,可得BC=AD=3EC,由勾股定理可求可求CE的长,由“AAS”可证△AB'F≌△DC'F,可得C'F=B'F=![]() ,即可求解.
,即可求解.
∵四边形ABCD是矩形,
∴AB=CD=1,AD=BC,∠B=∠C=90°
由折叠的性质可得:AB=AB'=CD=C'D=1,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,
∵点C'恰好为EB'的中点,
∴B'E=2C'E,
∴BE=2CE,
∴BC=AD=3EC,
∵AE2=AB2+BE2,DE2=DC2+CE2,AD2=AE2+DE2,
∴1+4CE2+1+CE2=9CE2,
∴CE=![]() ,
,
∴B'E=BE=![]() ,BC=AD=
,BC=AD=![]() ,C'E=
,C'E=![]() ,
,
∴B'C'=![]() ,
,
∵∠B'=∠DC'F=90°,∠AFB'=∠DFC',AB'=C'D,
∴△AB'F≌△DC'F(AAS),
∴C'F=B'F=![]() ,
,
∴EF=C'E+C'F=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
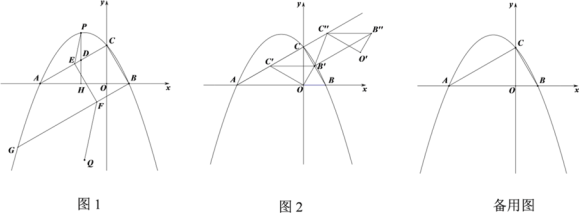
(1)如图1,求直线BC的解析式;
(2)如图1,线段AC上方抛物线上有一动点P,PD⊥x轴于点H,交线段AC于点D,直线BG∥AC,交抛物线于点G,点F是直线BC上一动点,FE∥BC交AC于点E,点Q是点A关于直线BG的对称点,连接PE、QF.当线段PD取最大值时,求PE+EF+QF的最小值及点E的坐标;
(3)如图2,将△BOC绕点O逆时针旋转至△B′O C′的位置,点B、C的对应点分别为点B′、C′,点B′恰好落在BC上.将△B′O C′沿直线AC平移,得到△B′′O ′ C′′,点B′、C′、O的对应点分别为点B′′、C′′、O ′,连接B ′ B′′、B ′C′′,△B ′B′′C′′是否能为等腰三角形?若能,请直接写出所有符合条件的C′′的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形ABCD中,E为边BC上的一点,AE⊥DE,AB=12,BE=16,F为线段BE上一点,EF=7,连接AF.如图1,现有一张硬纸片△GMN,∠NGM=900,NG=6,MG=8,斜边MN与边BC在同一直线上,点N与点E重合,点G在线段DE上.如图2,△GMN从图1的位置出发,以每秒1个单位的速度沿EB向点B匀速移动,同时,点P从A点出发,以每秒1个单位的速度沿AD向点D匀速移动,点Q为直线GN与线段AE的交点,连接PQ.当点N到达终点B时,△GMNP和点同时停止运动.设运动时间为t秒,解答问题:

(1)在整个运动过程中,当点G在线段AE上时,求t的值;
(2)在整个运动过程中,是否存在点P,使△APQ是等腰三角形,若存在,求出t的值;若不存在,说明理由;
(3)在整个运动过程中,设△GMN与△AEF重叠部分的面积为S,请直接写出S与t的函数关系式以及自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
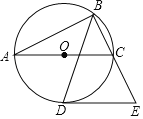
【题目】如图,以△ABC的边AC为直径的O恰为△ABC的外接圆,∠ABC的平分线交O于点D,过点D作DE∥AC交BC的延长线于点E
(1)求证:DE是⊙O的切线;
(2)若AB=4![]() ,BC=2
,BC=2![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考临近,某商家抓住商机,准备了一批考试专用笔及文具袋.去年五月份.笔的售价比文具袋的售价少2元,笔和文具袋的销售量都为100,结果笔与文具袋的总销售额为1400元.
(1)求去年五月份笔和文具袋的售价;
(2)受市场影响,该商家估计今年五月份购买笔的人会减少,于是降低了笔的售价,结果发现五月份笔的销售量有提升.经统计发现与去年五月份相比文具袋的售价每降价1元,文具袋的销售量就增加10件,同时笔的销售量就增加20件,且笔的售价不变.如果今年五月份笔和文具盒的总销售额比去年五月份的笔和文具盒的总销售额多90元,求今年五月份文具袋的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
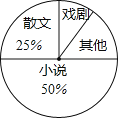
(1)计算m= ;
(2)在扇形统计图中,“其他”类所占的百分比为 ;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
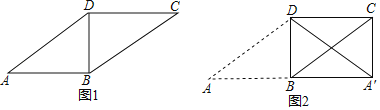
【题目】如图1,在平行四边形ABCD中,对角线BD⊥AB,以BD为对称轴将△ABD翻折,点A的对应点为A′,连接A′C,得到图2.
推理证明
(1)求证:四边形A′BDC是矩形;
实践操作
(2)在图1中将△ABD或△BDC进行平移、旋转或轴对称变换,重新构造一个特殊四边形.
要求:①画出图形,标明字母;②写出构图过程及构造的特殊四边形的名称.(不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com