
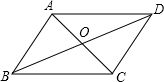
 如图,在?ABCD中,对角线AC与BD相交于点O,则图中共有4对全等三角形.
如图,在?ABCD中,对角线AC与BD相交于点O,则图中共有4对全等三角形. 分析 可以推出△ABD≌△CDB,△ABC≌△CDA,△AOB≌△COD,△AOD≌△COB.
解答 解:∵在△ABD和△CDB中
$\left\{\begin{array}{l}{AD=BC}\\{AB=CD}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠CBD,∠ABD=∠BDC,
∵在△ABC和△CDA中
$\left\{\begin{array}{l}{AD=BC}\\{AB=CD}\\{AC=CA}\end{array}\right.$,
∴△ABC≌△CDA(SSS),
∴∠DAC=∠BCA,∠ACD=∠BAC,
∵在△AOB和△COD中
$\left\{\begin{array}{l}{∠BAC=∠DCO}\\{AB=CD}\\{∠ABD=∠CDB}\end{array}\right.$,
∴△AOB≌△COD(ASA),
∵在△AOD和△COB中
$\left\{\begin{array}{l}{∠ADB=∠DBC}\\{AD=CB}\\{∠DAC=∠BCA}\end{array}\right.$,
∴△AOD≌△COB(ASA),
故答案为:4.
点评 此题主要考查了全等三角形的判定与性质,关键是判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠ACB=90°,AC=BC,点F在AB上,连接CF,AE⊥CF于E,BD垂直CF的延长线于点D.若AE=4cm,BD=2cm,则EF的长是( )
如图,在△ABC中,∠ACB=90°,AC=BC,点F在AB上,连接CF,AE⊥CF于E,BD垂直CF的延长线于点D.若AE=4cm,BD=2cm,则EF的长是( )| A. | $\frac{1}{3}$cm | B. | $\frac{2}{3}$cm | C. | 1cm | D. | $\frac{4}{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
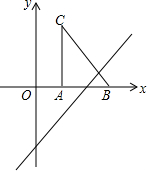 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x-5上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x-5上时,线段BC扫过的面积为( )| A. | 80 | B. | 88 | C. | 96 | D. | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A(n,-2),B(2,3)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$图象的两个交点
已知A(n,-2),B(2,3)是一次函数y1=kx+b的图象和反比例函数y2=$\frac{m}{x}$图象的两个交点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
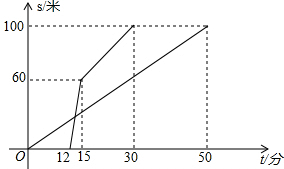 在“龟兔赛跑”中,兔子输给乌龟极不服气,所以它约乌龟再赛一场,以雪耻前辱.在这次赛跑中乌龟提高了速度,兔子也全力以赴.但兔子在跑步过程中腿受伤了,速度也由此减慢了,乌龟一直匀速跑到最后.如图是乌龟和兔子跑步的路程S(米)与乌龟出发的时间t(分)之间的函数图象.根据图象提供的信息解决问题:
在“龟兔赛跑”中,兔子输给乌龟极不服气,所以它约乌龟再赛一场,以雪耻前辱.在这次赛跑中乌龟提高了速度,兔子也全力以赴.但兔子在跑步过程中腿受伤了,速度也由此减慢了,乌龟一直匀速跑到最后.如图是乌龟和兔子跑步的路程S(米)与乌龟出发的时间t(分)之间的函数图象.根据图象提供的信息解决问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
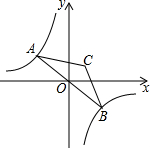 如图,点A是双曲线y=-$\frac{6}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为( )
如图,点A是双曲线y=-$\frac{6}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com