
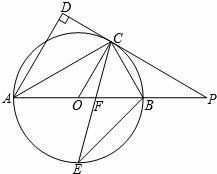
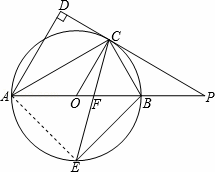
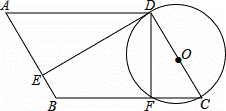
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若tan∠ABC=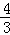 ,BE=7
,BE=7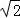 ,求线段PC的长.
,求线段PC的长.
解:(1)∵PD切⊙O于点C,
∴OC⊥PD.
又∵AD⊥PD,
∴OC∥AD.
∴∠ACO=∠DAC.
又∵OC=OA,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB.
(2)∵AD⊥PD,
∴∠DAC+∠ACD=90°.
又∵AB为⊙O的直径,
∴∠ACB=90°.
∴∠PCB+∠ACD=90°,
∴∠DAC=∠PCB.
又∵∠DAC=∠CAO,
∴∠CAO=∠PCB.
∵CE平分∠ACB,
∴∠ACF=∠BCF,
∴∠CAO+∠ACF=∠PCB+∠BCF,
∴∠PFC=∠PCF,
∴PC=PF,
∴△PCF是等腰三角形.
(3)连接AE.
∵CE平分∠ACB,
∴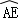 =
=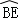 ,
,
∴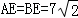 .
.
∵AB为⊙O的直径,
∴∠AEB=90°.
在Rt△ABE中,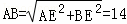 .
.
∵∠PAC=∠PCB,∠P=∠P,
∴△PAC∽△PCB,
∴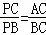 .
.
又∵tan∠ABC=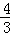 ,
,
∴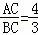 ,
,
∴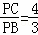 .
.
设PC=4k,PB=3k,则在Rt△POC中,PO=3k+7,OC=7,
∵PC2+OC2=OP2,
∴(4k)2+72=(3k+7)2,
∴k=6 (k=0不合题意,舍去).
∴PC=4k=4×6=24.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
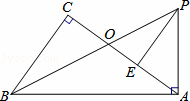
如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.
(1)求证:AP=AO;
(2)求证:PE⊥AO;
(3)当AE=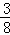 AC,AB=10时,求线段BO的长度.
AC,AB=10时,求线段BO的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
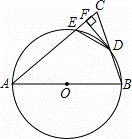
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,与边AC交于点E,过点D作DF⊥AC于F.
(1)求证:DF为⊙O的切线;
(2)若DE= ,AB=
,AB=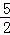 ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边AB相交于点E,且AE=3EB.
(1)求证:△ADE∽△CDF;
(2)当CF:FB=1:2时,求⊙O与▱ABCD的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
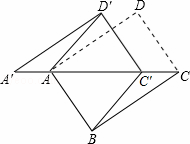
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A′C′D′.
(1)证明△A′AD′≌△CC′B;
(2)若∠ACB=30°,试问当点C'在线段AC上的什么位置时,四边形ABC′D′是菱形,并请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com