
【题目】某服装店因为换季更新,采购了一批新服装,有A、B两种款式共100件,花费了6600元,已知A种款式单价是80元/件,B种款式的单价是40元/件
(1)求两种款式的服装各采购了多少件?
(2)如果另一个服装店也想要采购这两种款式的服装共60件,且采购服装的费用不超过3300元,那么A种款式的服装最多能采购多少件?
【答案】(1)A种款式的服装采购了65件,B种款式的服装采购了35件;(2)A种款式的服装最多能采购22件.
【解析】
(1)设A种款式的服装采购了x件,则B种款式的服装采购了(100﹣x)件,根据总价=单价×数量结合花费了6600元,即可得出关于x的一元一次方程,解之即可得出结论;
(2)设A种款式的服装采购了m件,则B种款式的服装采购了(60﹣m)件,根据总价=单价×数量结合总费用不超过3300元,即可得出关于m的一元一次不等式,解之取其中最大的整数值即可得出结论.
解:(1)设A种款式的服装采购了x件,则B种款式的服装采购了(100﹣x)件,
依题意,得:80x+40(100﹣x)=6600,
解得:x=65,
∴100﹣x=35.
答:A种款式的服装采购了65件,B种款式的服装采购了35件.
(2)设A种款式的服装采购了m件,则B种款式的服装采购了(60﹣m)件,
依题意,得:80m+40(60﹣m)≤3300,
解得:m≤22![]() .
.
∵m为正整数,
∴m的最大值为22.
答:A种款式的服装最多能采购22件.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
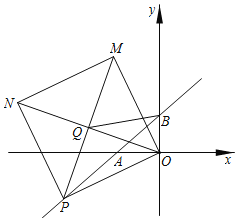
【题目】y=kx+b的图象经过点(﹣2,2)、(3,7)且与坐标轴相交于点、B两点.
(1)求一次函数的解析式.
(2)如图,点P是直线AB上一动点,以OP为边作正方形OPNM,连接ON、PM交于点Q,连BQ,当点P在直线AB上运动时,![]() 的值是否会发生变化?若不变,请求出其值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出其值;若变化,请说明理由.
(3)在(2)的条件下,在平面内有一点H,当以H、N、B、P为顶点的四边形为菱形时,直接写出点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏打算在某外卖网站点如下表所示的菜品和米饭.已知每份订单的配送费为3元,商家为促销,对每份订单的总价(不含配送费)提供满减优惠:满30元减12元,满60元减30元,满100元减45元.如果小敏在购买下表的所有菜品和米饭时,采取适当的下单方式,那么他的总费用最低可为( )
菜品 | 单价(含包装费) | 数量 | |
| 水煮牛肉(小) | 30元 | 1 |
| 醋溜土豆丝(小) | 12元 | 1 |
| 豉汁排骨(小) | 30元 | 1 |
| 手撕包菜(小) | 12元 | 1 |
| 米饭 | 3元 | 2 |
A.48元B.51元C.54元D.59元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线L:![]() 经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为
经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为![]() .
.
(1)求抛物线L的表达式;
(2)点P在抛物线![]() 上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与反比例函数
与反比例函数![]() (
(![]() >0)的图象分别交于点 A(
>0)的图象分别交于点 A(![]() ,4)和点B(8,
,4)和点B(8,![]() ),与坐标轴分别交于点C和点D.
),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当![]() 时,直接写出
时,直接写出![]() 的解集;
的解集;

(3)若点P是![]() 轴上一动点,当△COD与△ADP相似时,求点P的坐标.
轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(![]() ﹣1)0+2sin30°-
﹣1)0+2sin30°-![]() +|﹣2017|;
+|﹣2017|;
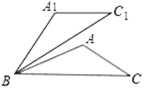
(2)如图,在△ABC中,已知∠ABC=30°,将△ABC绕点B逆时针旋转50°后得到△A1BC1,若∠A=100°,求证:A1C1∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(﹣2,﹣4),直线x=﹣2与x轴相交于点B,连接OA,抛物线y=﹣x2从点O沿OA方向平移,与直线x=﹣2交于点P,顶点M到点A时停止移动.
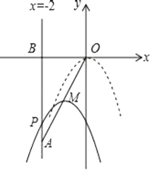
(1)线段OA所在直线的函数解析式是 ;
(2)设平移后抛物线的顶点M的横坐标为m,问:当m为何值时,线段PA最长?并求出此时PA的长.
(3)若平移后抛物线交y轴于点Q,是否存在点Q使得△OMQ为等腰三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年高一新生开始,某省全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考;“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考
(1)“1+2”的选考方案共有多少种?请直接写出所有可能的选法;(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)
(2)高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.
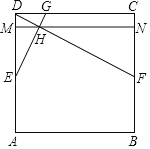
(1)猜想![]() 与
与![]() 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;
(2)过点![]() 作
作![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,若正方形
,若正方形![]() 的边长为10,点
的边长为10,点![]() 是
是![]() 上一点,求
上一点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com