
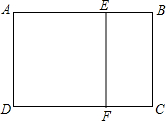
 如果一个矩形的宽与长的比是黄金比,那么这个矩形称为黄金矩形.如图,已知四边形ABCD为黄金矩形,以它的宽为边在其内部作正方形AEFD,那么剩下的矩形BCFE也是一个黄金矩形,你能证明这个结论吗?
如果一个矩形的宽与长的比是黄金比,那么这个矩形称为黄金矩形.如图,已知四边形ABCD为黄金矩形,以它的宽为边在其内部作正方形AEFD,那么剩下的矩形BCFE也是一个黄金矩形,你能证明这个结论吗?
| ||
| 2 |
| ||
| 2 |
3-
| ||
| 2 |
| BE |
| BC |
| ||||
|
3-
| ||
|
(3-
| ||||
(
|
2
| ||
| 4 |
| ||
| 2 |


科目:初中数学 来源: 题型:
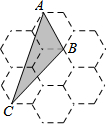 如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )A、2
| ||
| B、4 | ||
C、3
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 运输工具 | 途中速度/(km/h) | 途中费用/(元/km) | 装卸费用/元 | 装卸时间/h |
| 飞机 | 200 | 16 | 1000 | 2 |
| 火车 | 100 | 4 | 2000 | 4 |
| 汽车 | 50 | 8 | 1000 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
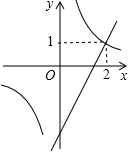 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com