
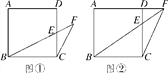
【题目】已知正方形ABCD,点E在边CD上,点F在线段BE的延长线上,连接FC,且∠FCE=∠CBE.
(1)如图①,当点E为CD边的中点时,求证:CF=2EF;
(2)如图②,当点F位于线段AD的延长线上时,求证: ![]() .
.
【答案】(1)见解析 (2)见解析
证明:(1)∵四边形ABCD是正方形,
∴CD=BC.∵点E为CD边的中点,
∴CE=![]() CD=
CD=![]() BC.
BC.
∵∠FCE=∠CBE,∠F=∠F,∴△FCE∽△FBC,
∴![]()
又∵CE=![]() BC,∴
BC,∴![]() =
=![]() ,∴CF=2EF.
,∴CF=2EF.
(2)∵四边形ABCD是正方形,∴DE∥AB,AD∥BC,AD=CD,∴ ![]() =
=![]() ,
,
∴![]() =
=![]() .∵AF∥BC,∴∠DFE=∠CBE.∵∠FCE=∠CBE,∴∠DFE=∠FCE.又∵∠FDE=∠CDF,∴△FDE∽△CDF,∴
.∵AF∥BC,∴∠DFE=∠CBE.∵∠FCE=∠CBE,∴∠DFE=∠FCE.又∵∠FDE=∠CDF,∴△FDE∽△CDF,∴![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
【解析】试题分析:根据正方形的性质得到![]() ,由点
,由点![]() 为
为![]() 边的中点,得到
边的中点,得到![]() 根据相似三角形的性质即可得到结论;
根据相似三角形的性质即可得到结论;
![]() 根据正方形的性质得到
根据正方形的性质得到![]() 根据平行线分线段成比例定理得到
根据平行线分线段成比例定理得到![]() 等量代换得到
等量代换得到![]() 根据相似三角形的性质得到
根据相似三角形的性质得到![]()
于是得到结论.
试题解析:(1)∵四边形ABCD是正方形,
∴CD=BC.
∵点E为CD边的中点,
![]()
∵∠FCE=∠CBE,∠F=∠F,
∴△FCE∽△FBC,
![]()
又∵![]()
![]()
∴CF=2EF.
(2)∵四边形ABCD是正方形,
∴DE∥AB,AD∥BC,AD=CD,
![]()
![]()
∵AF∥BC,
∴∠DFE=∠CBE.
∵∠FCE=∠CBE,
∴∠DFE=∠FCE.
又∵∠FDE=∠CDF,
∴△FDE∽△CDF,
![]()
![]()


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
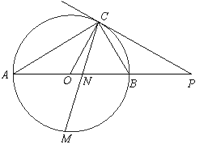
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生物学家发现了一种病毒,其长度约为0.00000032mm,数据0.00000032用科学记数法表示正确的是( )
A.3.2×107
B.3.2×108
C.3.2×10﹣7
D.3.2×10﹣8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点
,点![]() 、
、![]() 分别在直线
分别在直线![]() ,
,![]() 上,点
上,点![]() 为平面内一点.
为平面内一点.
(![]() )如图,
)如图,![]() ,
,![]() ,
,![]() 的数量关系是__________.
的数量关系是__________.

(![]() )利用(
)利用(![]() )的结论解决问题:如图,已知
)的结论解决问题:如图,已知![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,求
,求![]() 得度数.
得度数.

(![]() )如图,点
)如图,点![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,直接写出
,直接写出![]() ,
,![]() ,
,![]() 之间的数量关系.(用含
之间的数量关系.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解南京市民每天的阅读时间情况,随机抽取了部分市民进行调查,根据调查结果绘制如下尚不完整的频数分布表:
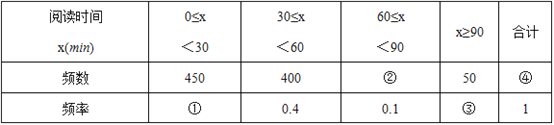
(1)补全表格中①~④的数据;
(2)将每天阅读时间不低于60min的市民称为“阅读爱好者”,若我市约有800万人,请估计我市能称为“阅读爱好者”的市民约有多少万人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com