
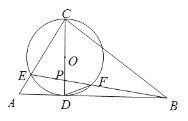
【题目】如图,△ABC中,∠ACB=90°,D为AB上的一点,以CD为直径的⊙O交AC于E,连接BE交CD于P,交⊙O于F,连接DF,∠ABC=∠EFD.
(1)求证:AB与⊙O相切;
(2)若AD=4,BD=6,则⊙O的半径= ;
(3)若PC=2PF,BF=a,求CP(用a的代数式表示).
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证明∠CDF+∠FDB=90°,即∠CDB=90°,即可证明AB与⊙O相切;
(2)证明△CBD∽△ADC,求出CD=2![]() ,即可得出⊙O的半径;
,即可得出⊙O的半径;
(3)证明△PCF∽△PBC,得出![]() ,根据已知可得PF=
,根据已知可得PF=![]() BF=
BF=![]() a,从而得到CP的值.
a,从而得到CP的值.
解:(1)∵∠ACB=90°
∴∠CBE+∠CEB=90°
∵∠ABC=∠EFD,
∠ABC=∠CBE+∠FBD
∠EFD=∠FDB+∠FBD
∴∠CBE=∠FDB
∵∠CEB=∠CDF
∴∠CDF+∠FDB=90°
即∠CDB=90°
∴AB与⊙O相切.
(2)∵∠ACD+∠BCD=90°
∠ACD+∠A=90°
∴∠BCD=∠A
∵∠BCD=∠ADC=90°
∴△CBD∽△ADC
∴![]()
∴CD2=AD![]() BD=4×6=24
BD=4×6=24
∴CD=2![]()
即⊙O的直径为2![]()
∴⊙O的半径为![]() .
.
故答案为![]() .
.
(3)∵CD是⊙O的直径
∴∠CFD=90°
∴∠CDF+∠DCF=90°
∵∠CDB=90°
∴∠CDF+∠FDB=90°
∴∠DCF=∠FDB
∵∠EBC=∠FDB
∴∠EBC=∠DCF
∴△PCF∽△PBC
∴![]()
∴PB=2PC=4PF
∵PB=BF+PF
∴PF=![]() BF=
BF=![]() a
a
∴PC=2PF=![]() a
a
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】某中学号召全校学生进行安全教育网络学习,并对部分学生的学习情况进行了随机调查.对部分学生的成绩(x为整数,满分100分)进行统计,并绘制了如下统计图表.
调查结果频数分布表
| 调查结果扇形统计图
|
根据所给信息,解答下列问题:
(1)填空:![]() _________,
_________,![]() _________;
_________;
(2)求扇形统计图中,m的值及A组对应的圆心角的度数;
(3)若参加学习的同学共有1500人,请你估计成绩不低于80分的同学有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
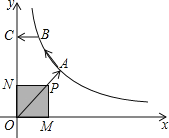
【题目】如图,已知点A是直线y=x与反比例函数y=(k>0,x>0)的交点,B是y=图象上的另一点,BC∥x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
A.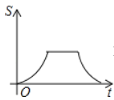 B.
B.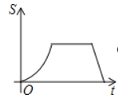 C.
C.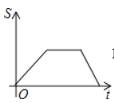 D.
D.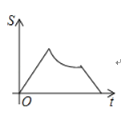
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖市某医院计划选购A,B两种防护服.已知A防护服每件价格是B防护服每件价格的2倍,用80000元单独购买A防护服比用80000元单独购买B防护服要少50件.如果该医院计划购买B防护服的件数比购买A防护服件数的2倍多8件,且用于购买A,B两种防护服的总经费不超过320000元,那么该医院最多可以购买多少件B防护服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在矩形ABCD中,AB=5,![]() ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
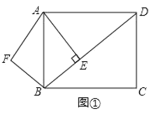
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,求出相应的m的值;
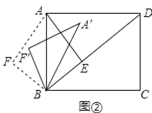
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的![]() 为
为![]() ,在旋转过程中,设
,在旋转过程中,设![]() 所在的直线与直线AD交于点P,与直线BD交于点Q,若△DPQ为等腰三角形,请直接写出此时DQ的长.
所在的直线与直线AD交于点P,与直线BD交于点Q,若△DPQ为等腰三角形,请直接写出此时DQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
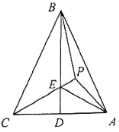
【题目】如图,P为等腰△ABC内一点,AB=BC,∠BPC=108°,D为AC中点,BD与PC相交于点E,已知P为△ABE的内心.
(1)求证:∠PEB=60°;
(2)求∠PAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com