
| A. | 2+$\sqrt{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 4+2$\sqrt{3}$或2-$\sqrt{3}$ | D. | 2+$\sqrt{3}$或2-$\sqrt{3}$ |
分析 分两种情形讨论:①当圆心O在△ABC内部时.②当点O在△ABC外时.分别求解即可.
解答 解:①当圆心O在△ABC内部时,作AE⊥BC于E.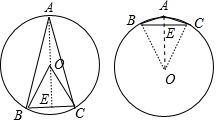
∵OB=OC,∠BOC=60°,
∴△OBC是等边三角形,
∴OB=OC=BC=2,
∴AE=OA+OE=2+$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$•BC•AE=$\frac{1}{2}$×2×(2+$\sqrt{3}$)=2+$\sqrt{3}$.
②当点O在△ABC外时,连接OA交BC于E.
S△ABC=$\frac{1}{2}$•BC•AE=$\frac{1}{2}$×2×(2-$\sqrt{3}$)=2-$\sqrt{3}$,
故选D.
点评 本题考查三角形的外接圆与外心、等腰三角形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,注意一题多解,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③ | C. | ①② | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | -$\sqrt{(-2)^{2}}$=2 | D. | $\root{3}{-8}$=-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
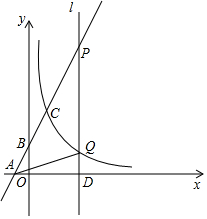 如图,在平面直角坐标系中,一次函数y=2x+2与x轴y轴分别交于点A,B与反比例函数y=$\frac{4}{x}$在第一象限交于点C.
如图,在平面直角坐标系中,一次函数y=2x+2与x轴y轴分别交于点A,B与反比例函数y=$\frac{4}{x}$在第一象限交于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com