
分析 (1)平均时间=$\frac{总时间}{7}$.
(2)第一种是费用=每分钟的费用×时间+通信费,第二种的费用=月费+通信费.
(3)将30×$\frac{2}{3}$小时分别代入(1)计算出费用的大小,再进行比较就可以得出结论.
解答 解:(1)该用户一周内平均每天上网的时间是:$\frac{32+40+36+42+35+47+48}{7}$=40(分钟).
答:该用户一周内平均每天上网的时间是40分钟.
(2)采用计时制应付的费用为0.1•x•60+0.2•x•60=18x(元),
采用包月制应付的费用为50+0.2•x•60=(50+12x)(元);
(3)若一个月内上网的时间为30×$\frac{2}{3}$=20小时,
则计时制应付的费用为18×20=360(元),
包月制应付的费用为50+12×20=290(元).
∵360>290
∴包月制合算.
点评 本题考查了一元一次方程的应用,表示费用的时候注意单位的统一.解决问题的关键是读懂题意,找到所求的量的等量关系.


科目:初中数学 来源: 题型:解答题
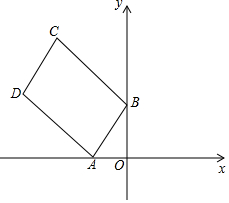 如图,在直角坐标系中,点A,B分别在x轴负半轴、y轴正半轴上,
如图,在直角坐标系中,点A,B分别在x轴负半轴、y轴正半轴上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),
如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P将线段AB分割成两条线段AP、PB,且AP:AB=PB:AP,那么点P就叫做线段AB的黄金分割点;若AB=3,那么AP的长为$\frac{-3+3\sqrt{3}}{2}$.
如图,点P将线段AB分割成两条线段AP、PB,且AP:AB=PB:AP,那么点P就叫做线段AB的黄金分割点;若AB=3,那么AP的长为$\frac{-3+3\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
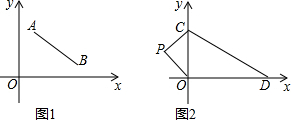
 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.
如图,在△ABC中,∠BAC=90°,AB=8,AC=6,线段BC所在的直线以每秒2个单位的速度,沿与其垂直的方向向上平行移动,设x秒时,该直线在△ABC内部的部分DE的长度为y,试写出y关于x的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
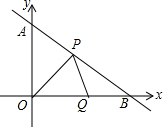 如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.
如图,直线y=-$\frac{3}{4}$x+3与y轴交于点A,与x轴交于点B,点P从点B出发以每秒1个单位长度的速度沿BA边向终点A运动,同时点Q以相同的速度从坐标原点O出发沿OB边向终点B运动,设点P运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,在平面直角坐标系中,A(1,a),B(b,1),其中a,b满足$\sqrt{2a-b-2}$+(a+b-7)2=0.
已知,在平面直角坐标系中,A(1,a),B(b,1),其中a,b满足$\sqrt{2a-b-2}$+(a+b-7)2=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com