
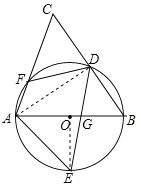
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=![]() ,E是弧AB的中点,求EGED的值.
,E是弧AB的中点,求EGED的值.

【答案】(1)见解析;(2)∠BDF=110°;(3)18
【解析】试题解析:(1)直接利用圆周角定理得出AD⊥BC,劲儿利用线段垂直平分线的性质得出AB=AC,即可得出∠E=∠C;
(2)利用圆内接四边形的性质得出∠AFD=180°﹣∠E,进而得出∠BDF=∠C+∠CFD,即可得出答案;
(3)根据cosB=![]() ,得出AB的长,再求出AE的长,进而得出△AEG∽△DEA,求出答案即可.
,得出AB的长,再求出AE的长,进而得出△AEG∽△DEA,求出答案即可.
试题解析:(1)证明:连接AD,∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC,∵CD=BD,∴AD垂直平分BC,∴AB=AC,∴∠B=∠C,又∵∠B=∠E,∴∠E=∠C;
(2)解:∵四边形AEDF是⊙O的内接四边形,∴∠AFD=180°﹣∠E,又∵∠CFD=180°﹣∠AFD,∴∠CFD=∠E=55°,又∵∠E=∠C=55°,∴∠BDF=∠C+∠CFD=110°;
(3)解:连接OE,∵∠CFD=∠E=∠C,∴FD=CD=BD=4,在Rt△ABD中,cosB=![]() ,BD=4,∴AB=6,∵E是
,BD=4,∴AB=6,∵E是![]() 的中点,AB是⊙O的直径,∴∠AOE=90°,∵AO=OE=3,∴AE=
的中点,AB是⊙O的直径,∴∠AOE=90°,∵AO=OE=3,∴AE=![]() ,∵E是
,∵E是![]() 的中点,∴∠ADE=∠EAB,∴△AEG∽△DEA,∴
的中点,∴∠ADE=∠EAB,∴△AEG∽△DEA,∴![]() ,即EGED=
,即EGED=![]() =18.
=18.


科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形平移与旋转”为主题开展数学活动,![]() 和
和![]() 是两个等边三角形纸片,其中,
是两个等边三角形纸片,其中,![]() .
.
解决问题
(1)勤奋小组将![]() 和
和![]() 按图1所示的方式摆放(点
按图1所示的方式摆放(点![]() 在同一条直线上) ,连接
在同一条直线上) ,连接![]() .发现
.发现![]() ,请你给予证明;
,请你给予证明;

(2)如图2,创新小组在勤奋小组的基础上继续探究,将![]() 绕着点
绕着点![]() 逆时针方向旋转,当点
逆时针方向旋转,当点![]() 恰好落在
恰好落在![]() 边上时,求
边上时,求![]() 的面积;
的面积;

拓展延伸
(3)如图3,缜密小组在创新小组的基础上,提出一个问题: “将![]() 沿
沿![]() 方向平移
方向平移![]() 得到
得到![]() 连接
连接![]() ,当
,当![]() 恰好是以
恰好是以![]() 为斜边的直角三角形时,求
为斜边的直角三角形时,求![]() 的值.请你直接写出
的值.请你直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场推出两种优惠方法,甲种方法:购买一个书包赠送一支笔;乙种方法:购买书包和笔一律按九折优惠,书包20元/个,笔5元/支,小明和同学需购买4个书包,笔若干(不少于4支).
(1)分别写出两种方式购买的费用y(元)与所买笔支数x(支)之间的函数关系式;
(2)如果商场允许可以任意选择一种优惠方式,也可以同时用两种方式购买,请你就购买4个书包12支笔,设计一种最省钱的购买方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受台风影响的区域.
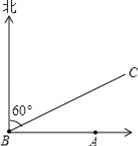
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四块完全相同的小长方形拼成的一个“回形”正方形.

(1)用不同代数式表示图中的阴影部分的面积,你能得到怎样的等式:________;
(2)利用(1)中的结论.计算:![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)根据(1)的结论.若![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式,例如:![]() ,
,![]() ,
,![]() ,…含有两个字母
,…含有两个字母![]() ,
,![]() 的对称式的基本对称式是
的对称式的基本对称式是![]() 和
和![]() ,像
,像![]() ,
,![]() 等对称式都可以用
等对称式都可以用![]() ,
,![]() 表示,例如:
表示,例如:![]() .
.
请根据以上材料解决下列问题:
(1)式子:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,属于对称式的是 (填序号)
中,属于对称式的是 (填序号)
(2)已知![]() .
.
①若![]() ,求对称式
,求对称式![]() 的值
的值
②若![]() ,求对称式
,求对称式![]() 的最大值
的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
(1)若∠B=50°,∠C=30°,则∠DAE= .
(2)若∠B=60°,∠C=20°,则∠DAE= .
(3)由(1)(2)猜想∠DAE与∠B,∠C之间的关系为 ,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两商场以同样价格出售同样的商品,并且各自又推出不同的优惠方案:
甲商场:购物超过200元后,超出200元的部分按90%收费;
乙商场:购物超过100元后,超出100元的部分按95%收费.
设小李在同一商场购买商品的原价总和为![]() 元,则甲商场消费的金额为
元,则甲商场消费的金额为![]() 元,乙商场消费的金额为
元,乙商场消费的金额为![]() 元.
元.
(1)请分别求出![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当![]() 元时,小李在哪家商场购物更合算?
元时,小李在哪家商场购物更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com