
【题目】如图,在四边形ABCD中,AD∥BC,AD=2,AB=2![]() ,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
(1)求∠ABE的大小及弧DEF的长度;
(2)在BE的延长线上取一点G,使得弧DE上的一个动点P到点G的最短距离为2![]() -2,求BG的长.
-2,求BG的长.

【答案】(1)∠ABE=45°,![]() ;(2)4.
;(2)4.
【解析】(1)连接AE,如图1,根据圆的切线的性质可得AE⊥BC,解Rt△AEB可求出∠ABE,进而得到∠DAB,然后运用圆弧长公式就可求出![]() 的长度;
的长度;
(2)如图2,根据两点之间线段最短可得:当A、P、G三点共线时PG最短,此时AG=AP+PG=2![]() =AB,根据等腰三角形的性质可得BE=EG,只需运用勾股定理求出BE,就可求出BG的长.
=AB,根据等腰三角形的性质可得BE=EG,只需运用勾股定理求出BE,就可求出BG的长.
(1)连接AE,如图1.
∵AD为半径的圆与BC相切于点E,∴AE⊥BC,AE=AD=2.
在Rt△AEB中,sin∠ABE=![]() =
=![]() =
=![]() ,∴∠ABE=45°.
,∴∠ABE=45°.
∵AD∥BC,∴∠DAB+∠ABE=180°,∴∠DAB=135°,∴![]() 的长度为
的长度为![]() =
=![]() ;
;
(2)如图2,根据两点之间线段最短可得:
当A、P、G三点共线时PG最短,此时AG=AP+PG=2+2![]() ﹣2=2
﹣2=2![]() ,AB=2
,AB=2![]() ,∴AG=AB.
,∴AG=AB.
∵AE⊥BG,∴BE=EG.
∵BE=![]() =
=![]() =2,∴EG=2,∴BG=4.
=2,∴EG=2,∴BG=4.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,AD∥BC,点
中,AD∥BC,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足为
的垂线,垂足为![]() 、
、![]() .
.

(1)求证:△AGE≌△CHF;
(2)连接![]() ,线段
,线段![]() 与
与![]() 请交于点M,若CH=4,GH=10,求△AGM的面积.
请交于点M,若CH=4,GH=10,求△AGM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小辉从家(点0)出发,沿着等腰三角形A0B的边0A-AB-B0的路径去匀匀速散步,其中0A=0B。设小辉距家(点0)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
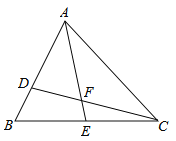
【题目】如图,D、E分别是△ABC边AB、BC上的点,AD=2BD,BE=CE,若S△ABC=18,设△ADF的面积为S1,△CEF的面积为S2,则S1-S2的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=33°,则∠CAD= °.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com