
分析 根据完全平方公式(a±b)2=a2±2ab+b2,即可解答.
解答 解:(1)$(\frac{3}{5}x+5y)^{2}=\frac{9}{25}{x}^{2}$+6xy+25y2,故答案为:5y.
(2)(3a+b)2=9a2+6ab+b2.故答案为:3a,6ab,b2.
(3)5022=(500+2)2=5002+2×500×2+22=252004.故答案为:500,2,5002+2×500×2+22,252004.
(4)∵(x-3)2=x2+kx+9,
∴k=2×(-3)=-6,
故答案为:-6.
(5)(a+1)2=a2+2a+1=1+1=2.
故答案为:2.
点评 本题考查了完全平方公式,解决本题的关键是熟记完全平方公式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
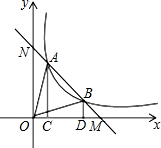 如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{2}{x}$交于点A(1,2),与x轴交于点M,与y轴交于点N.
如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{2}{x}$交于点A(1,2),与x轴交于点M,与y轴交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小军和小虎两人从同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米.小军骑自行车,小虎步行,当小军从原路返回到学校时,小虎刚好到达图书馆.图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
小军和小虎两人从同一条路同时从学校出发到图书馆查阅资料,学校与图书馆的路程是4千米.小军骑自行车,小虎步行,当小军从原路返回到学校时,小虎刚好到达图书馆.图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{3}{x}$,x≠0 | B. | y=$\frac{3}{x}$,x>0 | C. | y=$\frac{6}{x}$,x≠0 | D. | y=$\frac{6}{x}$,x>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com